問題PDF
神奈川県横浜市神奈川区にある浅野中学校は今年で創立100周年を迎えます。
浅野中学校にゆかりのあるマークを集めてみました。このとき、次の問いに答えなさい。

(1)
〔図3〕は、浅野中学校を表すマークです。
〔図3〕の「中」の形を一筆書きで書いたとき、書き方は全部で何通りありますか。
(2)
〔図4〕は横浜市を表すマークです。
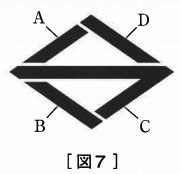
〔図7〕のようにA~Dの4つの部分を、赤・青・黄・緑の4色で塗り分けます。
使わない色があってもよいとき、塗り方は全部で何通りありますか。
ただし、AとCや、AとDのように隣り合う部分は異なる色を塗るものとします。
(3)
〔図5〕は神奈川県を表すマークで、1948年11月3日水曜日に制定されました。
浅野中学校の創立日は1920年1月20日ですが、この日は何曜日ですか。
ただし、現在の暦では、うるう年(2が29日までの年)は次の①、②のように決められています。
①西暦年号が4で割り切れる年とうるう年とする。
②①の例外として、西暦年号が100で割り切れて400で割り切れない年はうるう年ではないとする。
(4)
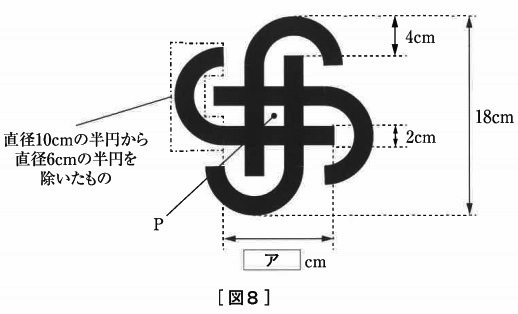
〔図8〕は、〔図6〕の神奈川区のマークを元に描いた図形です。
〔図8〕の〔 ア 〕にあてはまる数を求めなさい。
ただし、〔図8〕は、点Pに関して点対称になっています。
(5)
(4)の〔図8〕の黒い部分の面積は何cm2ですか。
@解説@
(1)
『中』の1筆書き。
行き止まりをスタートかゴールにする。
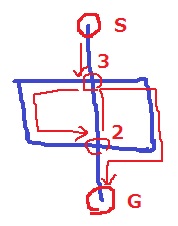
上をスタート、下をゴールとする。
最初の分岐で3通り、次の分岐で2通り→6通り
スタートとゴールが逆の場合を含めて12通り。
@@
クイズの方で一筆書きの法則を書きましたので、お時間のある方はぜひどうぞ。

(2)

マークをきちんと見ないと間違える。
CはA・B・Dすべてに接しているので、Cで場合分け。
Cを赤とする。Bは赤以外で3通り。
Aは赤以外で3通り、Dは赤とA以外で2通り→6通り
全部で3×6=18通り。
Cが青・黄・緑でも同様のことがいえる。
18×4=72通り
(3)
②のルールは使わない。
1948年11月3日が水曜日。ゴールは1920年1月20日。
1920年11月3日より、1919年11月3日の方がゴールに近いので後者の曜日を求める。
365÷7=52…1
1年は52週と1日だから、平年では1つ、うるう年では2つ曜日がズレる。
1948年から1919年は29年前。
その間にうるう年は、1920~1948(2月)のなかの4の倍数年なので、
(48-20)÷4+1=8回ある。
1948→1919では、29+8=37つ曜日がズレる。
37÷7=5…2
過去にさかのぼるときは、起点となる曜日(水)の手前から数える。
余り2は火→月。
1919年11月3日は月曜日。
1919年11月3日~1920年1月20日までの日数は、
(31-3+1)+31+20=79日間
79÷7=11…2
余り2は、月→火。
したがって、1920年1月20日は火曜日となる。

↑ちんちんに見える…。
(4)
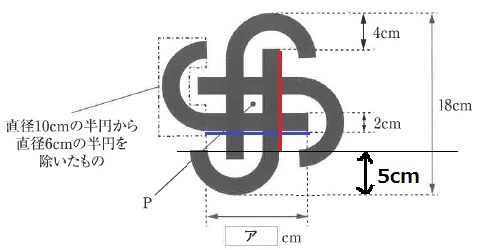
青の線と赤の線の長さが等しい。
大きい半円の半径は5cmだから、ア=18-(4+5)=9cm
(5)
扇形部分…(5×5×3.14-3×3×3.14)×2=32×3.14=100.48cm2
直線部分…9×2×4-2×2×4=56cm2
100.48+56=156.48cm2


コメント