問題ＰＤＦ
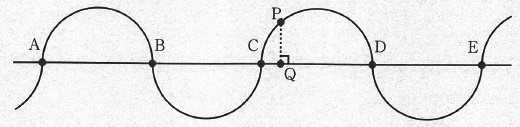
図のように、半径が5.4ｋｍの半円が４個つながっている形で流れている川があり、そこに橋Ａから橋Ｅがかかったまっすぐな道がある。川の水は、ＡからＥに向かって、時速1.8ｋｍの速さで流されている。川はどの部分も一定の速さで流れているものとする。また、道と川のはばと高低差は考えないものとする。円周率を３として、次の問いに答えなさい。
（１）
エンジンを停止した船をＡから川に流したとき、Ｂに着くまでに何時間かかりますか。
（２）
静水時に同じ速さの２そうの船を、ＡとＥから同時に出発させたとき、
出発から３時間後にＰで出会った。船の静水時の速さは時速何ｋｍですか。
（３）
（２）において、慶太君が自転車で船と同時にＡを出発し、Ｅに向かってまっすぐな道を一定の速さで走っていたところ、ちょうど２そうの船がＰで出会うのを、Ｑで進行方向の左側に90度の向きに見ることができた。慶太君の自転車の速さは時速何ｋｍですか。
＠解説＠
（１）
ＡＢ間（半円）の長さは、5.4×２×３÷２＝16.2ｋｍ
16.2ｋｍ÷時速1.8ｋｍ＝９時間
（２）
静水時の船の速さを●とする。
Ａから下る船の速さ＝●＋1.8
Ｅから上る船の速さ＝●－1.8
この２つが出会いにいく。
１時間あたりに近づく距離は、（●＋1.8）＋（●－1.8）＝●×２
つまり、静水時の速さの２倍。
ＡＥ間は半円４つ分なので、16.2×４＝64.8ｋｍ
●＝64.8ｋｍ÷３時間÷２＝時速10.8ｋｍ
（３）
Ａから出発する船は、10.8＋1.8＝時速12.6ｋｍで進む。
進んだ距離は、時速12.6ｋｍ×３時間＝37.8ｋｍ
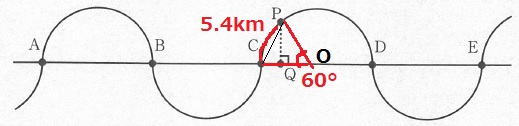
半円は16.2ｋｍなので、弧ＣＰの長さは、37.8－16.2×２＝5.4ｋｍ
中心角ＰＯＣ＝180×5.4/16.2＝60°
△ＰＯＣは正三角形となり、ＣＱはＣＯの半分となる。
慶太が進んだ距離は、5.4×４＋5.4÷２＝24.3ｋｍ
24.3ｋｍ÷３時間＝時速8.1ｋｍ
難関中（算数科）解説ページに戻る
コメント