問題PDF
T地点を頂点とする五角すいの形をした山があります。図のように、五角すいの辺はすべて道になっていて、山の高さの3分の1、3分の2の高さにも五角形の道があります。A地点とB地点の間には展望台が、C地点とD地点の間には茶屋があります。S地点から出発していずれかの道を通ってT地点まで行きます。ただし、同じ地点、同じ道は通らず、上から下には進まないものとします。

〔 〕にあてはまる数を求めなさい。ただし、同じ記号の欄には同じ数字が入ります。
(1)
AB間の展望台を必ず通ることにすると、
SからAまでの行き方は〔 ア 〕通り、
BからTまでの行き方は〔 イ 〕通りなので、
SからTまで展望台を通って行く行き方は〔 ア 〕×〔 イ 〕通りあります。
(2)
CD間の茶屋を必ず通ることにすると、
SからCまでの行き方は〔 ウ 〕通りなので、
DからTまでの行き方は〔 イ 〕通りなので、
SからTまで茶屋を通って行く行き方は〔 ウ 〕×〔 イ 〕通りあります。
(3)
SからTまでの行き方は〔 エ 〕通りあります。
@解説@
(1)
Sから直接Aに向かうか向かわないかで場合分け。
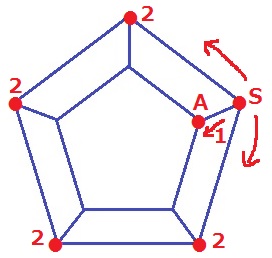
Sから直接Aに向かうのが1通り。
他の頂点は右回りか左回りかで2通りずつ。
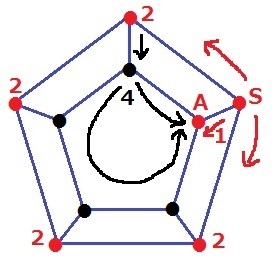
小さい五角形の頂点●からAに向かうには、右回りと左回りで2通りずつ。
●を経由すると2×2=4通り
●は4つあるのですべて足すと、1+4×4=17通り(ア)
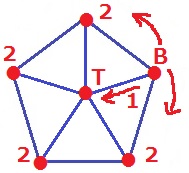
同様に、1+2×4=9通り(イ)
(2)
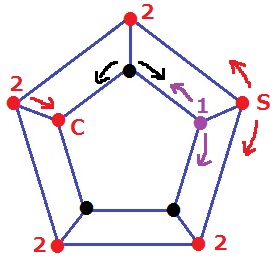
はじめにSから内側の五角形に移動(●)してC→1×2=2通り
Cに近い●からC→2通り
●を経由してC→2×2×3=12通り
合計で16通り。
(3)
わざわざ(1)と(2)で場合分けされているので、前問の解答を用いる。
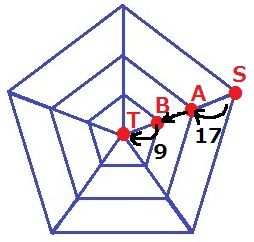
S→A→B→T経由だと、17×9=153通り

S→C→D→T経由は16×9=144通り
これは●にもいえるので、144×4=576通り
したがって、153+576=729通り



コメント