2017年度　早稲田中学過去問２回目【算数】大問２解説

問題ＰＤＦ
（１）
図の四角形ＡＢＣＤは正方形です。アの角の大きさは何度ですか。

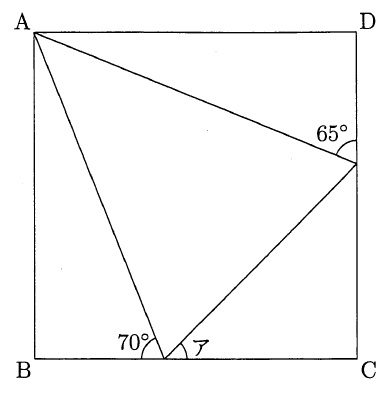
（２）
図の四角形ＡＢＣＤは平行四辺形です。
影がついた部分ア、イ、ウの面積は、順に35ｃｍ²、99ｃｍ²、15ｃｍ²です。
斜線部分の面積は何ｃｍ²ですか。

（３）
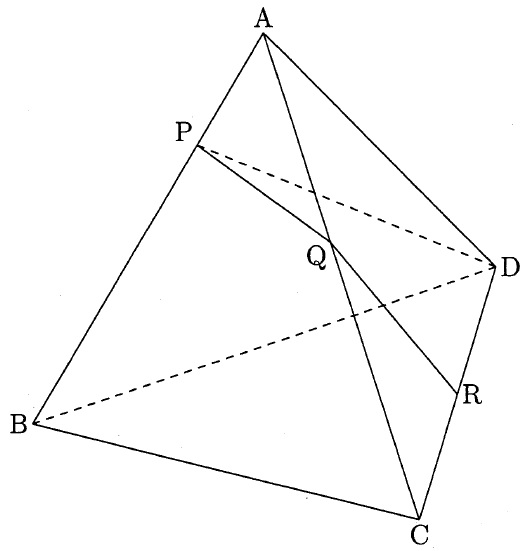
図の三角すいはすべての面が正三角形で、１つの面の面積は18ｃｍ²です。
点Ｐ、Ｑ，Ｒはそれぞれ辺ＡＢ、ＡＣ、ＣＤ上の点で、点Ｒは辺ＣＤの真ん中の点です。
３つの辺ＤＰ、ＰＱ、ＱＲの長さの和が最も短くなるとき、
三角形ＡＰＱの面積は何ｃｍ²ですか。

＠解説＠
（１）
もはや頻出の知識問題。

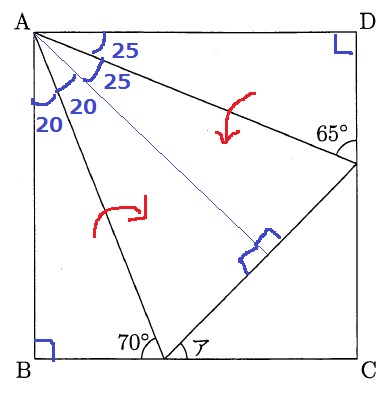
角度を調査すると、上の直角三角形と左の直角三角形の残りの角が25°と20°
和が45°からあいだの角も45°となり、２つの直角三角形を内側に折るとピッタリ重なる！

なぜそうなるのか…。

△ＡＤＥを時計回りに90度回転させ、ＡＤとＡＢが接着するように回転移動する。
正方形の１辺よりＡＤ＝ＡＢ、∠ＡＢＦ＝90°だからＦＣは一直線。
∠ＥＡＤ＝∠ＦＡＢ＝25°
１辺と両端角が等しいので、△ＡＤＥと△ＡＢＦは合同。
ＡＥ＝ＡＦ

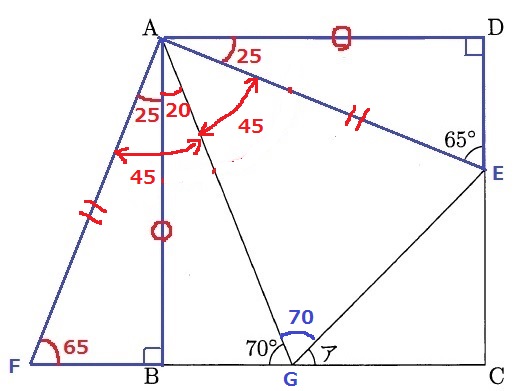
続いて、△ＡＦＧと△ＡＥＧに着目する。
∠ＦＡＧ＝∠ＥＡＧ＝45°、ＡＦ＝ＡＥ、ＡＧ＝ＡＧ（共通辺）
２辺と間の角度が等しいので、△ＡＦＧと△ＡＥＧは合同。
（△ＡＤＥ＋△ＡＢＧ＝△ＡＦＢ＋△ＡＧＢ＝△ＡＦＧ
→ＡＧを対称の軸として△ＡＦＧを対称移動→△ＡＥＧ
だから、先のように２つの直角三角形を内側へ折ると△ＡＥＧとピッタリ重なる）
∠ＡＧＥ＝70°より、ア＝180－70×２＝40°
*入試では知識としてすぐ使えるように準備しておく。

（２）
悩みまくりました(;`ω´)
共通部分を足して面積比かな？と思ったのですが、全体を俯瞰ふかんした方が良いです。

まず、おさえておきたいのは、△ＡＢＥと△ＢＦＣは平行四辺形の半分ずつであること。
Ｄへ等積変形すると各々平行四辺形の半分に相当し、合計すると平行四辺形の面積になる。

白い部分をＡ～Ｄとする。
（Ａ＋99＋Ｄ）＋（Ｂ＋99＋Ｃ）＝平行四辺形の面積
平行四辺形から斜線部分以外を引けば斜線部分がでる。

（Ａ＋99＋Ｄ）＋（Ｂ＋99＋Ｃ）－（Ａ＋Ｂ＋Ｃ＋Ｄ＋35＋99＋15）
＝99－35－15＝49ｃｍ²

（３）
最短距離の問題なので展開図を作成。

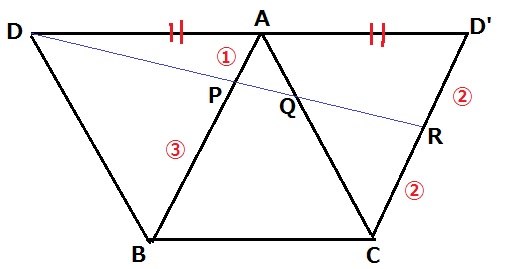
△ＤＡＰと△ＤＤ’Ｒは相似。
ＤＡ＝ＡＤ’より、ＡＰ＝①とすると、Ｄ’Ｒ＝②
ＲはＤ’Ｃの中点なので、正三角形の１辺は④となる。
ＰＢ＝④－①＝③

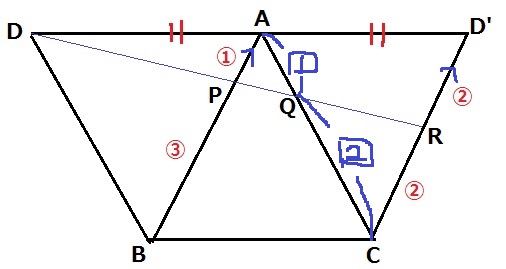
△ＡＰＱと△ＲＣＱの相似から、
ＡＱ：ＱＣ＝ＡＰ：ＣＲ＝１：２
隣辺比で、△ＡＰＱ＝18×（１×１）/（４×３）＝３/２ｃｍ²
難関中（算数科）解説ページに戻る