2020年度　栄光学園中学過去問【算数】大問２解説

問題ＰＤＦ
時針（短針）・分針（長針）・秒針がすべてなめらかに動く時計があります。
この時計の針と針のなす角について、次の問に答えなさい。
ただし、針と針のなす角とは、２本の針が作る角のうち、
その大きさが180度以下のものを指します。
例えば、下の図において、時針と分針のなす角とは、印のつけた角のことです。

（１）
１時間23分45分での、時針と秒針のなす角の大きさを答えなさい。

（２）
12時０分０秒に、時針・分針・秒針の３本はぴったり重なります。
この次に時針と分針がぴったり重なる時刻について考えます。
①12時０分０秒からこの時刻までに、時針は何度動きましたか。

②この時刻での、時針と秒針のなす角の大きさを答えなさい。

（３）
時針・分針・秒針の３本がぴったり重なるとき以外で、
時針と分針がぴったり重なるときを考えます。
これらの時刻の、時針と秒針のなす角のうち、最も小さいものの大きさを答えなさい。

（４）
時針・分針・秒針の３本がぴったり重なるとき以外で、
いずれかの２本がぴったり重なるときを考えます。
これらの時刻の、重なっている２本の針ともう１本の針とのなす角のうち、
最も小さいものの大きさを答えなさい。

＠解説＠
（１）

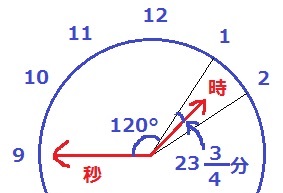
時針は１分あたり、30÷60＝0.5度ずつ動く。
23分45秒＝23・３/４分
時針が文字盤の１から動いた角度は、0.5×23・３/４＝11・７/８度
120＋11・７/８＝131・７/８度

（２）①
12時０分０秒から時針と分針が重なる時刻を求める。
１分あたり、時針は0.5度、分針は６度ずつ動く。
12時～１時までは重ならないので、１時以降を考える。
１時０分の時点で時針と分針は30度離れており、１分あたり６－0.5＝5.5度ずつ近づく。
30÷5.5＝60/11分後（時刻でいえば１時５・５/11分）
時針が動いた角度は、30＋0.5×60/11＝32・８/11度

②
１時５・５/11分のときの秒針の位置を特定する。
秒針は１分あたり360度動くので、
５/11分では360×５/11＝163・７/11度動く（文字盤の５と６の間）。
163・７/11－32・８/11
＝162・18/11－32・８/11＝130・10/11度

（３）
すべて調べ上げるのは途方に暮れる(;´Д｀)
そこで前問の答えを活用する。

時針・分針・秒針が重なる０時00分00秒からスタート。
時針と分針が重なるのは65・５/11分後の１時５・５/11分。
このとき、時針分針と秒針のズレは130・10/11度であった。

次に時針と分針が重なるのは、60÷5.5をして２時10・10/11分。
つまり、同じく65・５/11分後である。
ということは、秒針が移動する角度が同じなので、
時針分針と秒針とのズレの大きさも同じでは？
◆２時10・10/11分
130・10/11×２＝260・20/11＝261・９/11度
求めたいのは小さい方の角度だから、
360—261・９/11＝359・11/11－261・９/11＝98・２/11度

◆３時16・４/11分
130・10/11×３＝390・30/11＝392・８/11度
392・８/11－360＝32・８/11度

◆４時21・９/11分
130・10/11×４＝520・40/11＝523・７/11
523・７/11－360＝163・７/11度

◆５時27・３/11分
130・10/11×５＝650・50/11＝654・６/11
720－654・６/11＝719・11/11－654・６/11＝65・５/11度

◆６時32・８/11分
130・10/11×６＝780・60/11＝785・５/11
785・５/11－720＝65・５/11度
さっきと一緒⊂(^ω^)⊃

0時00分00秒から始まり、65・５/11分ごとに時針と分針が重なり、
12時00分00秒で再び時針と分針と秒針の３つが重なる。
反対に、12時00分00秒から65・５/11分前ごとに時針と分針が重なり、
00時00分00秒で再び時針と分針と秒針の３つが重なる。
つまり、時針と分針が重なるときの３つの針の位置関係は左右対称になる。
◆７時38・２/11分のときのズレは４時21・９/11分と同じ163・７/11度。
◆８時43・７/11分は３時16・４/11分と同じ32・８/11度。
◆９時49・１/11分は２時10・10/11分と同じ98・２/11度。
◆10時54・６/11分は１時５・５/11分と同じ130・10/11度。
結局、半分だけを調べればいいことになる。
したがって、32・８/11度。

（４）
（３）では時針と分針が重なったとき、これと秒針との間の角を求めた。
他には時針と秒針が重なり、これと分針との間の角、
もしくは分針と秒針が重なり、これと時針との間の角があるが、
すべてを調べ上げるのは大変困難:;(∩´＿`∩);:

思うに、動くスピードは秒針＞分針＞時針の順で速い。

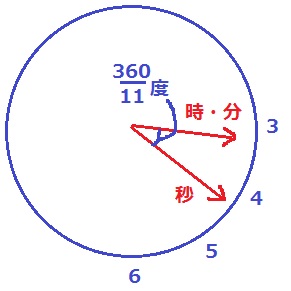
↑（３）３時16・４/11分の様子。
針のズレは32・８/11＝360/11度
秒針は文字盤の12から、360×４/11＝130・10/11度の位置にあるので、
文字盤の４～５の間にあるから時針と分針の下にいる。

ここから逆再生して時針と秒針を重ねる。
時針と分針は動きが鈍いので、そのあいだの角は大きくならない。
つまり、時針と秒針が重なり、これと分針との間の角が答えになる。

１秒あたりの角度を求める。
秒針は360÷60秒＝６度
分針は１分６度だから、６÷60＝１/10度
時針は１分0.5度だから、0.5÷60＝１/120度

留意すべき点は、秒針を戻すと時針も少し動くこと！
１秒あたり秒針は時針に、６－１/120＝719/120度近づく。
両者の距離は360/11度離れているので、360/11÷719/120＝360/11×120/719…
計算がヤバイので保留。
求めたいのは分針との角。
１秒あたり分針は時針から、１/10－１/120＝11/120度離れていく。
この360/11×120/719秒後を求める。

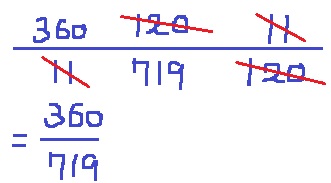
360/719度
どうなることやらと思いきや、最後はスッキリ+.*:ヽ(･∀･)ﾉ:･:*.+
難関中（算数科）解説ページに戻る