平均49.5点(前年比;-3.5点)
問題はこちら→リセマムさん
出題範囲の削減はなし。
大問1(計算)
(1)
-2×3+8
=-6+8
=2
(2)
2(2a-b)+3(a+2b)
=4a-2b+3a+6b
=7a+4b
(3)
(√5-1)(√5+4)
=5+4√5-√5-4
=1+3√5
(4)
x2-36
=(x+6)(x-6)
(5)
x2+3x+1=0
解の公式を適用して、
x=(-3±√5)/2
大問2(文字式)
L=2πr ←÷2π
r=L/(2π)
大問3(反比例)
反比例の比例定数aは積xyで一定。
a=12
y=12/x
大問4(平面図形)
(1)

半径でOB=OC→△OBCは二等辺三角形
∠OCB=57°
半円の弧に対する円周角ACB=90°だから、
x=90-57=33°
(2)
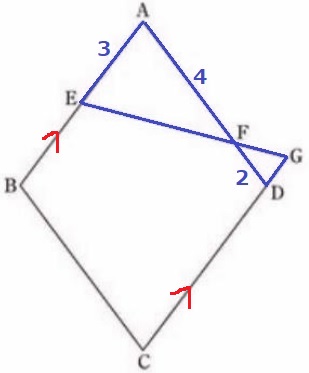
菱形ゆえ、AB//GC
△AEF∽△DGFから、DG=3×2/4=3/2cm
大問5(平面図形2)
(1)
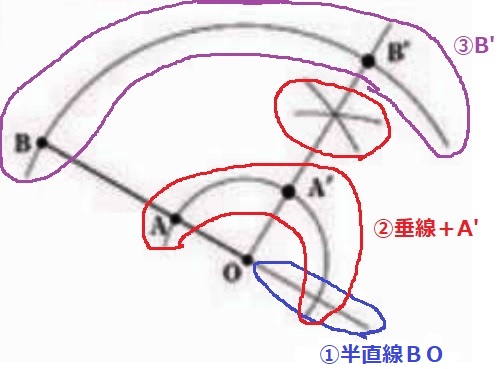
①BOを延長。
②Oを通る半直線BOの垂線。OAの長さを移してA’
③OBの長さを垂線に移してB’
(2)
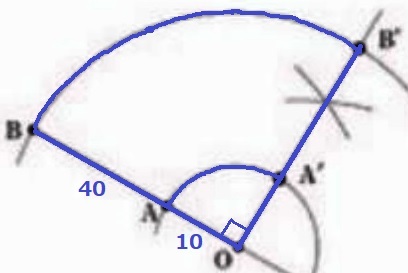
半径50cmの扇形から半径10cmの扇形を引けばいい。
50×50×π×1/4-10×10×π×1/4
=(50×50-10×10)×π×1/4
=2400×1/4×π
=600πcm2
大問6(方程式)
答案では文字が何を表すか示して方程式をつくり、過程を記述する。
家庭ごみの排出量をx、資源ごみの排出量をyとする。
x+y=680 …①
0.7x+0.8y=680-195=485 ←10倍
7x+8y=4850…②
②-①×7をすると、y=90
①に代入、x=680-90=590
家庭ごみ…590g、資源ごみ…90g
大問7(平面図形3)
△AFD≡△CGEの証明。

仮定よりAD=CEなので、この両端角に目を付ける。
FD//BEの同位角と対頂角(×)
AB//GCの錯角(●)
1辺と両端角が等しいので合同。
大問8(データの活用)
(1)
最頻値(モード)は最もあらわれている値。
28.0~29.0の階級値である28.5秒。
(2)
問題文に『14人の記録の平均値は、ちょうど27.5秒でした』とある。
27.5秒を仮の平均におく。
6人と仮の平均との差の合計は、
-2+0+0.6+1.4+2.7+3.3=6
6÷20=0.3
平均は、27.5+0.3=27.8秒
大問9(確率)
答案では理由も記述する。
■れん
2回のくじで1曲ずつ選ぶが、結局は5曲の中から2曲を選ぶので確率は2/5
■るい
ポップスは3曲から1曲選ばれるので1/3
2/5>1/3だから、Aが選ばれやすいのはれんさんの方法。
大問10(数量変化)
(1)
表Ⅰより、2分で16℃上昇している。
1分あたり8℃の上昇→変化の割合は8
(2)
表Ⅱより、2分で24℃上昇→y=12x+15
これにy=95を代入すると、x=20/3
強火の電気料金は、0.6×20/3=4円
表Ⅲより、2分で8℃上昇→y=4x+15
これにy=95を代入すると、x=20
弱火の電気料金は、0.2×20=4円
強火…4円、弱火…4円、同じ
@余談@
強火;y=12x+15
弱火;y=4x+15
変化の割合が強火:弱火=12:4=3:1
切片の始まりが15℃で、特定の温度まで到達する時間は逆比で強火:弱火=1:3
(表ⅡとⅢの39℃を見てみよう。強火は2分、弱火は6分。
(0、15)を原点に置き換えれば比例とみなせる)
1分あたりの電気料金が強火:弱火=0.6:0.2=3:1
特定の温度までの電気料金は強火:弱火=(1×3):(3×1)=1:1で同じ。
大問11(関数)
(1)
y=1/2x2にx=4を代入して、
y=1/2×42=8
(2)
■Bのx座標がAのx座標より大きい場合。

Bのx座標をaとする。(a>4)
B(a、1/2a2)
青線が35cm。これを変形させると赤線の長方形の周に相当する。
(1/2a2+a)×2=35
a2+2a=35
a2+2a-35
=(a+7)(a-5)=0
a>4より、a=5
■Bのx座標がAのx座標より小さい場合。

Bのx座標をbとする。
Bのy座標はAのy座標より大きくないと周の長さが足りなくなるので、
Oとbの距離は4を超える。(b<-4)
赤線の長方形の周で立式。縦は1/2b2、横はb+4
{1/2b2+(b+4)}×2=35
b2+2b+8=35
b2+2b-27=0
解の公式を適用。bの係数が偶数なので、b=2b’が使える。
b=1±2√7
b<-4より、b=1-2√7
答えは5、1-2√7
大問12(空間図形)
(1)
対角線AGではなく、図Ⅱの展開図における線分AGの長さを求める。
AH=2+4=6cm、HG=3cm
△AHGで三平方→AG=3√5cm
(2)

図Ⅱの△AEP∽△GFPより、
EP:FP=AE:GF=1:2
EP=3×1/3=1cm
Pを図Ⅰに記す。
三角錐GーAEPの体積は、1×2÷2×4÷3=4/3cm3
●講評●
大問1
基本の計算問題。オール死守。
大問2・3
中1分野。時間をかけずに正解する。
大問4・5
基本。ワイパーは線分の回転移動。
大問6
計算処理もしやすかった。
大問7
合同の証明は辺の長さに着目する。
AD=CEがきたら、その両端角に目星をつけてみる。
2組の平行線を活用。
大問8
(2)全部を合計して÷20でも出せる。
仮の平均の考え方もおさえておこう。
大問9
れん・るいの確率を提示して比較すればOK。
大問10
(2)時間をかけすぎないように。
大問11
(2)本試験最大の難問。
まずは問題文のとおりに形を図示する。
2辺を平行移動すれば長方形→(縦+横)×2=周の長さ35
もう1個が難しい。縦は1/2b2、横はb+4になる。
解の公式⇒Bのx座標が-4より下にあることで値が確定する。
大問12
(2)展開図でPの位置を確認→立体を作図。
処理もやりやすい。



コメント