2020年度　開智中学・先端Ａ過去問【算数】大問４解説

問題ＰＤＦ
あるクラスで100点満点の算数のテストを行ったところ、
クラスの生徒全員の平均点は75.5点でした。
100点をとった生徒は４人いて、その４人を除いた残りの生徒の平均点は72点でした。
テストの得点はすべて０以上100以下の整数であるとして、以下の問いに答えなさい。
（１）
このクラスの人数は全部で何人ですか。

（２）
平均点より高い得点をとった生徒は、もっとも多くて何人ですか。

同じクラスで100点満点の国語のテストを行ったところ、平均点は60.5点でした。
算数のテストで自分がとった点数以上の点数を国語のテストでとった人は、
ちょうど10人いました。

（３）
算数、国語の両方のテストでともに平均点より高い点数をとって生徒は、
もっとも多くて何人ですか。

＠解説＠
*入試では（２）（３）は考え方も解答用紙に書く。
（１）

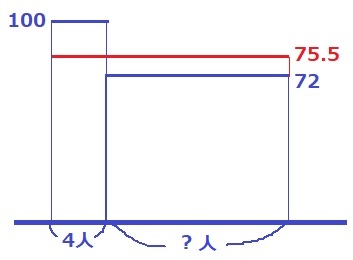
左が満点の４人。右がその他の？人。
２つの長方形を均すと75.5点になる。

４人の75.5点以上の面積が、その他の72点以上75.5以下と同じ。
（100－75.5）×４＝24.5×４＝98
？＝98÷（75.5－72）＝98÷3.5＝28
４＋28＝32人

（２）
クラス全員の平均は75.5点だった。
平均よりも高い点数をとった生徒を多くするには、
平均点よりギリギリ上の76点の生徒を増やす。

その他28人の総和…72×28＝2016点
これを76で割り、その整数部分が76点の得点者。
2016÷76＝26.5…→26人
26＋４＝30人
*26人の総和は、76×26＝1976点
残りの２人で2016－1976＝40点を適当に配分すればいい。

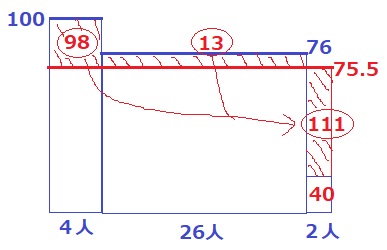
図を描くとこうなる。

（３）
（２）のように、総和から条件に適合するように得点を配分する。
クラス全員の総和…60.5×32＝1936点
『国語で算数以上の点数をとった人は10人』
言い換えれば、算数より国語で点が下がった人は22人もいる。
平均点の高い算数より、平均点の低い国語が悪かった人は多いので、
『国語で算数以上の点数をとった10人』を優先してつくる。

まず、先ほどの算数で平均以下だった２人が、国語で同じ点数を取る。
２人の総和…40点
算数で76点だった26人のうち、８人が国語で76点をとる。
８人の総和…76×８＝608点
これで、『国語が算数以上の10人』が完成。

残りの22人で、1936－（40＋608）＝1288点を分配する。
国語のギリ平均超えである61点の得点者を増産。
1288÷61＝21…≒21人

21人の総和…61×21＝1281点
残りの１人は、1288－1281＝７点となる。
したがって、算国両方で平均超えは、最も多くて８＋21＝29人
難関中（算数科）解説ページに戻る