問題PDF
星子さんは
9×9、99×99、999×999、9999×9999、99999×99999
を計算してみたところ、計算結果に規則性があることに気が付きました。
以下の問いに答えなさい。
(1)
999×999を計算しなさい。
(2)
各位の数がすべて9である100桁の数をaとするとき、
a×aを計算した結果の数について、各位の数の和を求めなさい。
(3)
各位の数がすべて3である100桁の数をbとします。
このとき、次の計算をした結果の数について、各位の数の和を求めなさい。
(ア)b×b (イ)b×b×2
@解説@
(1)
999×999=998001
@@
中3レベルの数学では、999=1000-1になおして、
999×999=(1000-1)2
=10002-2×1000×1+1×1=998001
(2)
100桁×100桁の計算結果をきかれてビビるが、
問題文に『計算結果に規則性がある』とあるので規則をさぐる。
試しに4桁を計算して、3桁と比較すると…
999×999=998001
9999×9999=99980001
求めるのは、”計算結果の各位の和”
3桁では27、4桁では36と9の倍数×桁数と同じになる!
よって、100桁×100桁では9×100=900
筆算で示すと、
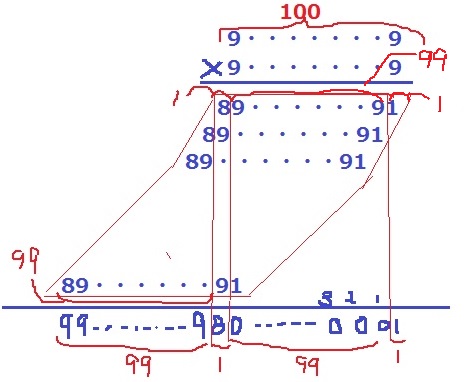
100桁の9×9をすると、積は101桁になる。
左が8、右が1、あいだに9が99個連なり、これが100段続く。
上図はうまく描けなかったが…赤い四角形は平行四辺形になる。
計算結果は9と0が99個ずつ、8と1が1個ずつで、
9×99+8+1=9×(99+1)=900
(3)ア
333×333=110889→和は27(9×3)
3333×3333=11108889→和は36(9×4)
よって、100桁の3×100桁の3→和は9×100=900
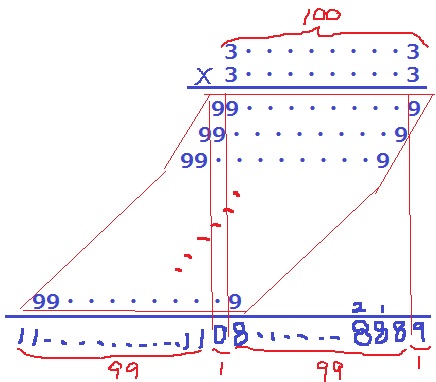
これも正確に描けば、平行四辺形になる。
(1+8)×99+9=9×(99+1)=900
イ
先ほどの計算結果を2倍する。
333×333=110889
110889×2=221778→和は27
3333×3333=11108889
11108889×2=22217778→和は36
先ほどと変わらない。
よって、900。
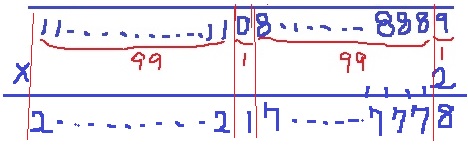
2が99個、7が99個、1と8が1個ずつ。
(2+7)×99+1+8
=9×(99+1)=900



コメント