問題PDF
太郎君と次郎君は駅を8時に出発し、同じ速さで歩いて学校に向かいました。その途中、駅から528m歩いたところにバス停Aがあります。太郎君はそのまま歩いて学校に向かい、8時41分に学校に着きました。次郎君はバス停Aから8時21分発のバスに乗りました。バスは8時23分に太郎君を追いぬき、学校を通り過ぎてバス停Bに8時28分に着きました。バスを降りた次郎君はそこから歩く速さの1.5倍の速さで走って学校の方にもどったところ、太郎君と同時に学校に着きました。
(1)
太郎君の歩く速さとバスの速さの比を最も簡単な整数の比で表しなさい。
(2)
駅から学校までの距離を求めなさい。
@解説@
(1)
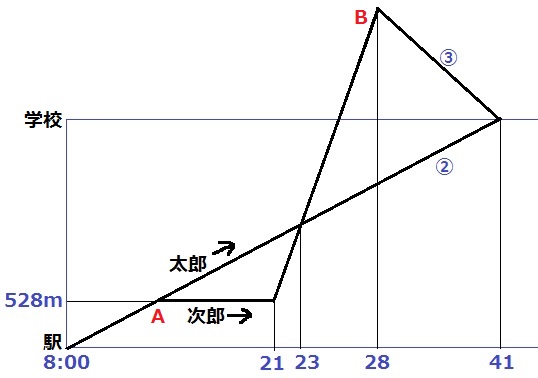
ダイヤグラムを作成する。
バス停Aに2人が着いた時刻は不明だが、ここで次郎だけがバスを待つ。
21分に発車して23分に太郎を追い越す。学校を通り過ぎ、28分にバス停Bに到着する。
それ以降の速さの比は、太郎:次郎=1:1.5=②:③
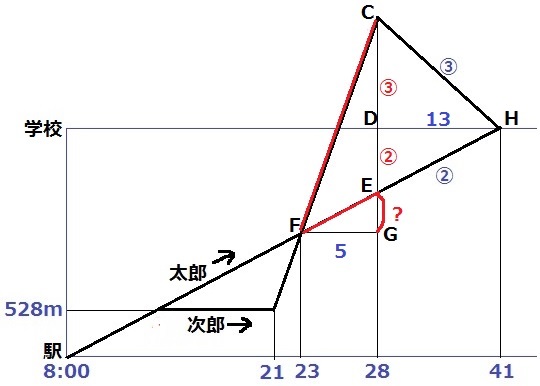
(↑点C~Hを打ちました)
バスと太郎の速さの比が知りたい。バスが走る時間のうち、赤線部分に注目しよう。
時間が同じ5分なので、この間の距離の比がわかれば速さの比を知れる。
最後の13分は時間一定→速さの比=距離の比で、CD:DE=③:②
FGに補助線。△EFGと△EHDは相似。
EG=②×5/13=〇10/13
CG=③+②+〇10/13=〇75/13
太郎:バス=EG:CG
=〇10/13:〇75/13=2:15
(2)

手がかりは駅―バス停A間の528mしかない。
次郎がバス停Aで待ち始めるIの時間がわかれば学校までの距離が求まる。
前問の速さの比を活用する。
JKに補助線。太郎のI、次郎のJから合流地点(交点)までは距離一定。
時間の比は速さの逆比で、IK:JK=15:2
JKがちょうど2分なので、IJは13分。
Iの時刻は8時21分の13分前だから8時8分。
太郎は8時41分に学校に着くので、528×41/8=2706m



コメント