問題ＰＤＦ
Ａ君とＢさん、Ｃ君とＤさんがそれぞれ２人１組のチームを作り、20ｋｍ先のゴールを目指して歩きます。Ａ君とＣ君が１人で歩くときの速さはそれぞれ時速６ｋｍ、ＢさんとＤさんが１人で歩くときの速さはそれぞれ時速３ｋｍです。また、Ａ君とＢさんが２人で一緒に歩くときの速さは時速５ｋｍです。
各チームは２人同時にスタートします。スタート後、２人で一緒に歩いても別々に歩いてもかませいませんが、立ち止まったり引き返したりはできません。スタートしてからゴールするまでにかかった２人の時間の合計（以下、チームの合計タイムとよびます）を考えます。
【例１】
Ａ君とＢさんのチームがスタートからゴールまで２人で一緒に歩いた場合、
20÷５＋20÷５＝８なので、チームの合計タイムは８時間０分です。
【例２】
Ａ君とＢさんのチームがはじめの15ｋｍは一緒に歩き、残りの５ｋｍは別々に歩いた場合、
（15÷５＋15÷５）＋（５÷６＋５÷３）＝8.5なので、チームの合計タイムは８時間30分です。
Ｃ君とＤさんのチームはスタートからゴールまで２人で一緒に歩いた場合でも、
スタートからゴールまで別々に歩いた場合でも、チームの合計タイムは変わりません。
このとき、次の問いに答えなさい。
（１）
Ａ君とＢさんのチームが、スタートからゴールまで２人で一緒に歩いた場合と、
スタートからゴールまで２人が別々に歩いた場合のチームの合計タイムの差は何時間何分ですか。
（２）
Ｃ君とＤさんのチームが２人で一緒に歩くときの速さは時速何ｋｍですか。
（３）
Ａ君とＢさんはスタートからある地点まで一緒に歩き、その後別々に歩いた場合、
チームの合計タイムは、Ｃ君とＤさんのチームの合計タイムより15分短くなりました。
Ａ君とＢさんが一緒に歩いたのはスタートから何ｋｍの地点までですか。
（４）
Ａ君とＢさんはスタートしてから別々に歩いていましたが、Ａ君はＢさんのことが心配になり、ルール違反ではあるがある地点で引き返し、Ｂさんと出会うと再びゴールを目指して２人で一緒に歩きました。すると、チームの合計タイムはＣ君とＤさんのチームの合計タイムと同じになりました。Ａ君が引き返した地点は、スタートしてから何ｋｍの地点ですか。
＠解説＠
（１）
ＡとＢが一緒に歩く→【例１】の通り、８時間０分。
ＡとＢが別々に歩く→20÷６＋20÷３＝10時間０分
差は２時間０分。
（２）
ＣとＤが別々に歩いたとする。
合計タイムは、20÷６＋20÷３＝10時間０分
ＣとＤがスタートからゴールまで一緒に歩いても合計タイムは10時間０分となる。
１人あたり５時間で20ｋｍを歩くので、20÷５＝時速４ｋｍ
（３）
ＣとＤのチームの合計タイムがどこにも書かれていない！
ＣとＤはスタートからゴールまで一緒に歩いても別々に歩いても合計タイムは10時間０分なので、
途中で別々に歩いた場合、どこで別れても10時間０分なのでは？と予想を立ててみる。
Ｃだけ：時速６ｋｍ Ｄだけ：時速３ｋｍ ＣＤ一緒：時速４ｋｍ
時間の比は速さの逆比。
時間の比→Ｃだけ：Ｄだけ：ＣＤ一緒＝１/６：１/３：１/４＝②：④：③
合計タイムの比は、ＣＤ別々：ＣＤ一緒＝（②＋④）：（③×２）＝１：１
一定の距離における合計タイムの比が等しいので、
合計タイムは20ｋｍに関係なく常に等しくなる。
すなわち、どこで別れても一緒に歩いた距離と別々に歩いた距離における、
それぞれの合計タイムの比が等しいので、ＣＤの合計タイムは10時間で一定となる。
ＡＢの合計タイムを10時間から15分（１/４時間）短くすればいい。
Ａだけ：時速６ｋｍ Ｂだけ：時速３ｋｍ ＡＢ一緒：時速５ｋｍ
時間の比→Ａだけ：Ｂだけ：ＡＢ一緒＝１/６：１/３：１/５＝⑤：⑩：⑥
ＡＢ別々：ＡＢ一緒＝（⑤＋⑩）：（⑥×２）＝⑮：⑫＝⑤：④
（１）より、ＡＢ別々の⑤は10時間、ＡＢ一緒の④は８時間で２時間の差がでる。
ＡとＢの合計タイムの最大値は10時間、最小値は８時間でこの範囲に収まる。
早々に別れると10時間に、ゴール付近で別れると８時間に近づく。
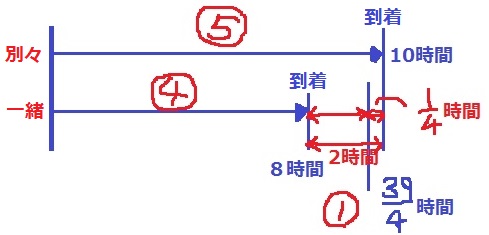
↑数直線は時間の長さ。
20ｋｍフルを別々で10時間。そこから15分（１/４時間）減らすには、
差の【２時間分】のうち、【１/４時間】に相当する距離を一緒に歩く距離に切り替えればいい。
20ｋｍ×1/4 / ２＝2.5ｋｍ
よって、ＡとＢが一緒に歩いたのはスタートから2.5ｋｍの地点まで。
*⑤と④の比は使わなかった(;`ω´)
できるだけ一緒に歩いた方が合計タイムは少なくなるとイメージしてください。
時間の比は次で使います。
（４）
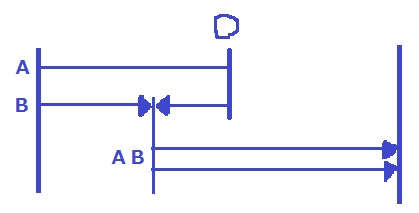
歩いた様子を線分図で示すと、このような感じ。
Ａが引き返した○を求めたい。
ポイントは、スタートから一緒に歩いた場合との２時間差に注目。
Ａが引き返してＢと出会う地点までの歩き方が違ったことで合計タイムが２時間伸びた。
一定の距離における時間の比は、Ａだけ：Ｂだけ：ＡＢ一緒＝⑤：⑩：⑥
気をつけるべき点は、Ａの速さはＢの２倍で、Ａ一人は同じ時間に２倍の距離を歩いていること！
（⑩と⑥は同じ距離だが、⑤は２倍の距離）
⑩＋⑤×２＝⑥×２＋２時間
⑳＝⑫＋２時間
⑧＝２時間
ＡとＢが別々に歩いたところ（上の黒い枠線）が⑳なので、２時間×⑳/⑧＝５時間
つまり、Ａが引き返し、ＡとＢが出会うまでの合計タイムは５時間。
１人あたりの時間では５/２時間。
この間、２人は（時速３ｋｍ＋時速６ｋｍ）×５/２時間＝45/２ｋｍ歩き、
Ａがスタートしてから引き返すまでの距離（往路）は、その半分。
したがって、Ａが引き返した地点はスタートから45/４ｋｍの地点となる。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント