問題PDF
データの特徴を調べるとき、次の値を考えることができます。
(1)
20人の生徒に5点満点の算数のテストを行ったところ、結果は以下の表のようになりました。

このテストの点数について、平均値と中央値をそれぞれ求めなさい。
(2)
20人の生徒に5点満点の国語のテストを行ったところ、結果は以下の表のようになりました。

このあと、太郎君と花子さんが同じテストを受けました。この2人の生徒の結果を加えたところ、
平均値は20人のときと変わらず、最頻値が4点となりました。
花子さんの方が太郎君より点数が高いとき、太郎君のテストの点数は何点ですか。
(3)
7人の生徒に100点満点の英語のテストを行ったところ、
7人の得点は以下のようになりました。(単位は点)
50、73、90、34、62、81、45
このあと、中野さんが同じテストを受けました。中野さんを加えた8人の生徒の結果を
確認したところ、7人のときと比べて中央値が2点下がりました。
中野さんのテストの点数は何点ですか。
@解説@
(1)

生徒の合計点は、0×1+1×4+2×2+3×3+4×7+5×3=60点
平均点は、60÷20=3点
20人の中央値は10番目と11番目の平均。
10番目が3点、11番目が4点なので中央値は3.5点。
平均値…3点、中央値…3.5点
(2)
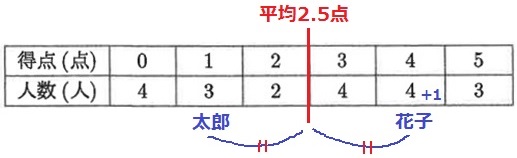
平均点は、(0×4+1×3+2×2+3×4+4×4+5×3)÷20=50÷20=2.5点
4点が最頻値で最も人数が多くなる→得点の高い花子が4点。
平均点は変動しない→太郎と花子の平均が2.5点→太郎と花子は2.5からの距離が等しい。
太郎は1点
(3)
データを昇順に並べ替える。
【34、45、50、62、73、81、90】
7人の中央値は4番目→62点
中野さんを加えると、中央値は62-2=60点になった。
中央値が下がったので中野さんは60点未満。
8人の中央値は4番目と5番目の平均。
60に最も近い62点が5番目、中野さんは4番目で60-2=58点



コメント