問題ＰＤＦ
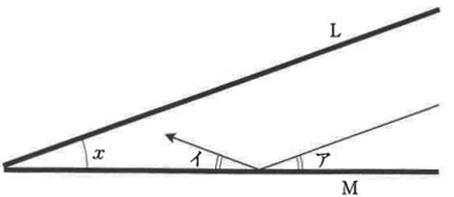
２つの鏡ＬとＭではさまれた区域があります。ＬとＭがつくる角の大きさはｘです。
図のように、光線はＬと平行に入ってきて、鏡に反射して直進します。
ただし、光線が鏡に反射するときには、図のように角アと角イが等しくなります。
（１）
ｘが30°のとき、光線は鏡に何回か反射して、ＬとＭのどちらかと平行に出ていきます。
それは何回で、ＬとＭのどちらと平行ですか。
（２）
ｘが20°のときも、光線は鏡に何回か反射して、ＬとＭのどちらかと平行に出ていきます。
それは何回で、ＬとＭのどちらと平行ですか。
（３）
光線が、鏡に何回か反射してＬと平行に出ていくのは、ｘが次のうちどの角度のときですか。
すべて選びなさい。
〔５° 15° 25° 35° 45° 55° 65° 75° 85°〕
＠解説＠
（１）
反射の問題は鏡の世界をつくる。
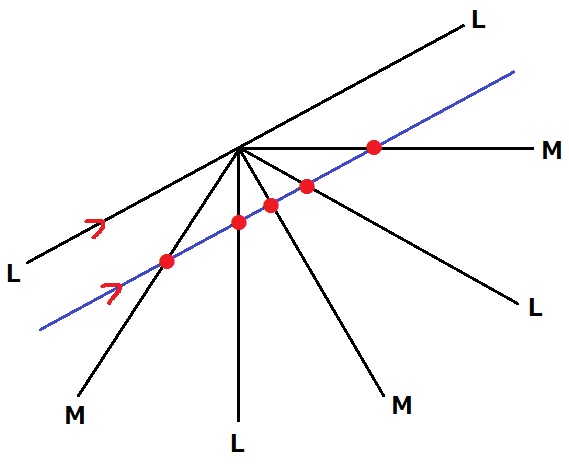
光はＬと平行に入ってくる。
最初のＬを基準として時計回りに30°の角を６個並べると180°になる。
この一直線と光は平行で交点がなくなり、光が反射しなくなる。
交点の数は５個→反射の回数は５回。
時計回りにＬ・Ｍ・Ｌ…と打っていくと、最後はＬと平行である。
５回、Ｌ
（２）
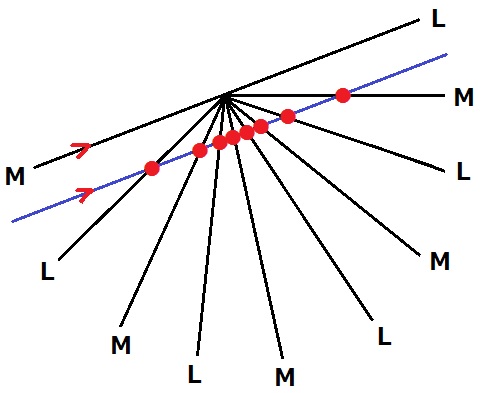
同様に調べる。
180÷20＝９個の角を合わせると光と平行になる。
交点の数は８個→反射は８回。最後はＭと平行。
８回、Ｍ
＠余談＠
反射の回数は〔角の個数－１〕回。
（３）
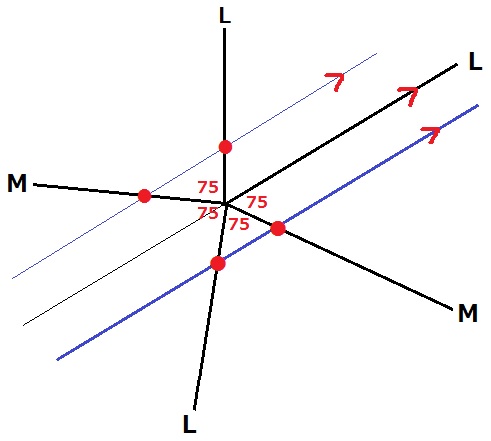
たとえば75°だと平行線が作れない。
鏡Ｌか鏡Ｍに対して光が平行にならないので、どこかで反射が続いてしまう。
180の約数である角でなければ光線は平行に出ていかない。
この時点で５°、15°、45°に絞られる。
前問を振り返ると、角の個数が偶数個でＬ平行、奇数個でＭ平行となる。
180÷５＝36個→Ｌ平行
180÷15＝12個→Ｌ平行
180÷45＝８個→Ｌ平行
全部Ｌ平行！
よって、５°、15°、45°。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント