問題ＰＤＦ
直線上に点Ａ、Ｂがあり、ＡとＢの間は30ｃｍです。
直線上のＡとＢの間を、点Ｐと点Ｑがそれぞれ動きます。
点ＰはＡを出発しＢに向かい、同時に点ＱはＢを出発しＡに向かいます。
点Ｐ、Ｑは出会ったら向きを変えて進みます。
点Ｐも点Ｑも、ＡまたはＢにたどり着いたら向きを変えて進みます。
ただし、点ＱはＢにたどり着いたとき、２秒間止まってから再び動き出します。
点Ｐ、Ｑの速さはそれぞれ一定です。
また、グラフは点Ｐの移動の様子の一部を表したものです。
（１）
点Ｐ、Ｑの速さはそれぞれ毎秒何ｃｍですか。
（２）
点Ｐ、Ｑが７回出会うまでに点Ｐが進んだ長さの合計は何ｃｍですか。
＠解説＠
（１）
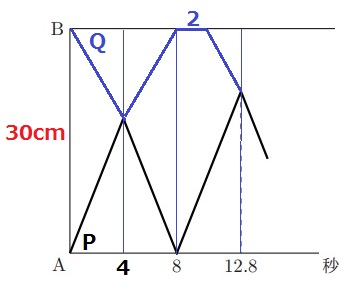
ＰとＱは出会うとトンボ帰りする。
行きと同じ速度で帰るので、はじめのグラフは上下対称になる。
１回目の出会いは８÷２＝４秒後
ＰとＱの速さの合計は30ｃｍ÷４秒＝毎秒7.5秒
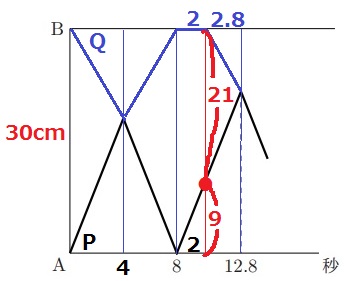
２回目の出会いまでＰは4.8秒、Ｑは2.8秒動く。
Ｐ、Ｑが一緒に動いたときの距離の和は、毎秒7.5ｃｍ×2.8秒＝21ｃｍ
Ｐだけが動いた距離は、30－21＝９ｃｍ
Ｐの速さは、９÷２＝毎秒4.5ｍ
Ｑの速さは、7.5－4.5＝毎秒３ｃｍ
（２）
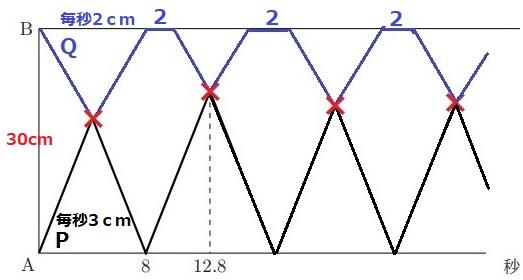
Ｐの方が速く、Ｑは２秒の待機があるので、ＱがＡに到着することはない。
ＰがＱより２秒余分に動いたとしても、12.8秒後のようにＰはＢに着くことなくＡへ戻る。
→ＰはＢ、ＱはＡに絶対到着できない。
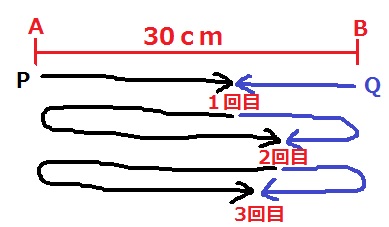
ＰとＱが動いた距離の和をみると、１回目の出会いまでが30ｃｍ。
２回目が30×３、３回目が30×５ｃｍ…
７回目の出会いまでに30ｃｍ×（２×７－１）＝390ｃｍ動く。
この間にＱは６回休憩するので、Ｐだけが動いた距離は、4.5×２×６＝54ｃｍ
ＰとＱが一緒に動いたときの距離の和は、390－54＝336ｃｍ
ＰとＱの速さの比＝距離の比は、4.5：３＝３：２
したがって、Ｐが動いた距離は、54＋336×３/５＝255.6ｃｍ
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント