問題ＰＤＦ
下の＜図１＞のように、同じ大きさの正方形のタイルが９枚並んでいます。
これらのタイルに色をぬる方法が何通りあるかを考えます。
例えば、４枚のタイルに色をぬる場合、
＜図２＞と＜図３＞は違う向きから見ると同じぬり方になるので、１通りと数えます。
また、＜図２＞と＜図４＞は違う向きから見ても同じぬり方にはならないので、
それぞれ異なるぬり方と考えます。このとき、次の各問いに答えなさい。
（１）
２枚のタイルに色をぬる方法は何通りありますか。
（２）
３枚のタイルに色をぬる方法は何通りありますか。
＠解説＠
（１）
９マスから塗る２マスを選ぶ→9Ｃ2＝36通り
ここから回転して重複するパターンを除外する。
回転すると４パターンできる。÷４すれば重複を回避できる。
注意点は、回転させても２パターンしかないものがあること！
そこで、以上の４通りについては別枠としてカウントする。
（36－４）÷４＝８通り
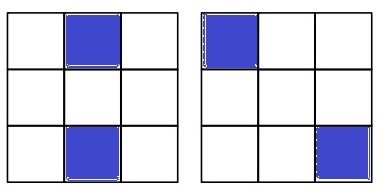
別枠は回転の重複を除くと２通りだから、８＋２＝10通り
（２）
仕組みがわかれば前問と一緒。
９マスから３マスを選ぶ→9Ｃ3＝84通り
回転させても４パターンにならないものは別枠で処理。
（84－４）÷４＋２＝22通り
難関中（算数科）解説ページに戻る
コメント