問題ＰＤＦ
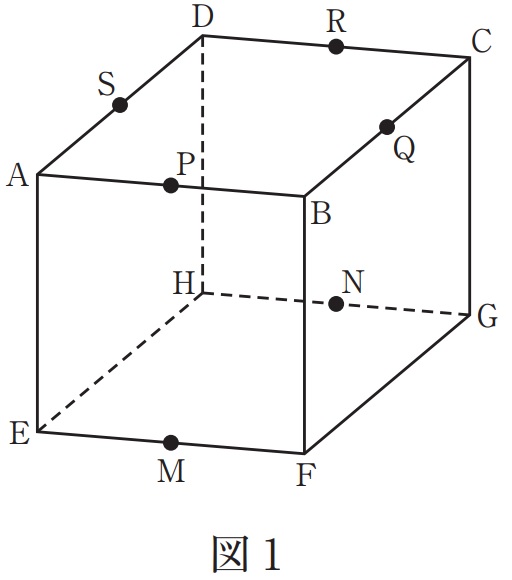
図１のような１辺が６ｃｍの立方体ＡＢＣＤ―ＥＦＧＨがあり、Ｐ、Ｑ、Ｒ、Ｓ、Ｍ、Ｎは辺の真ん中の点です。いくつかの点を結んでできる、図２のような三角柱ア（ＰＥＦーＲＨＧ）、イ（ＭＢＡ―ＮＣＤ）、ウ（ＱＦＧ―ＳＥＨ）を考えます。次の問いに答えなさい。ただし、角すいの体積は（底面積）×（高さ）÷３で求められるものとします。
（１）
アとイの共通部分（どちらの三角柱にもふくまれている部分）の体積を求めなさい。
（２）
アとウの共通部分（どちらの三角柱にもふくまれている部分）の体積を求めなさい。
（３）
イとウの共通部分（どちらの三角柱にもふくまれている部分）の体積を求めなさい。
＠解説＠
（１）
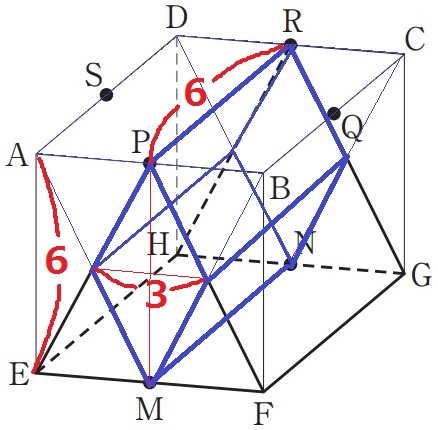
底面が菱形（対角線が３ｃｍと６ｃｍ）で高さ６ｃｍの四角柱。
３×６÷２×６＝54ｃｍ3
（２）
ＰＲ、ＳＱの中点をＯとする。
ＱＧを正面（面ＢＦＧＣ）から見て、奥にある面ＰＦＧＲに押し込むとＯＧになる。
ＱＦを面ＰＦＧＲに押し込むとＯＦになる。
同様に、ＳＨを面ＰＥＨＲに押し込むとＯＨに、ＳＥはＯＥになる。
Ｅ・Ｆ・Ｇ・Ｈから伸びる４つの線分がＯに集まり、求積すべき立体は正四角錘ＯーＥＦＧＨ。
６×６×６÷３＝72ｃｍ3
（３）
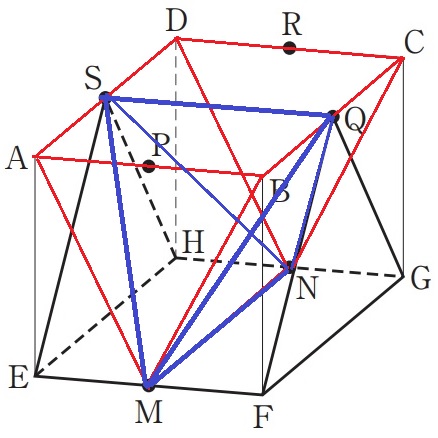
これも押し込んで考える。
面ＳＥＦＱにＡＭを押し込むとＳＭに、ＢＭを押し込むとＱＭにプリントアウトされる。
同様に、面ＳＨＧＱにＣＮはＱＮに、ＤＮはＳＨにプリントアウトされる。
求積すべき立体は四面体ＭＮＱＳ。
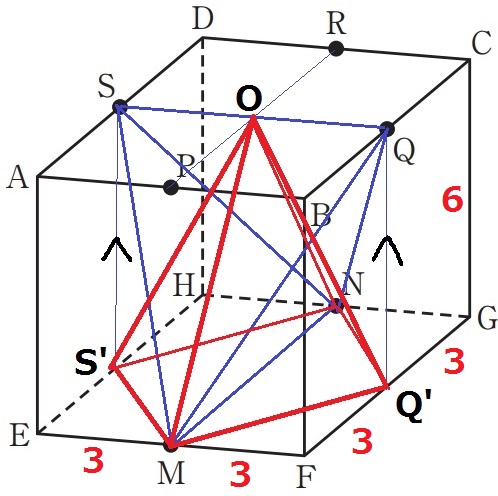
Ｓ、Ｑを真下に下ろした交点をそれぞれＳ’、Ｑ’とする。
面ＯＭＮに平行となるように四面体ＭＮＱＳを等積変形すると、正四角錘ＯーＭＱ’ＮＳ’になる。
（２）の正四角錘ＯーＥＦＧＨと高さが同じで底面積が半分だから体積は半分。
72÷２＝36ｃｍ3
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント