問題ＰＤＦ
同じ大きさの正方形の板が９枚あります。
これらの板には３種類の模様がかかれていて、
これらを向きを変えずに、たてと横にそれそれ３枚ずつ並べて模様を作ります。
例えば、下の図１、図２、図３のような模様が考えられます。
図２の模様は図１の模様を回転したものですが、違う模様とみなします。
図３の模様は、点対称であり線対称でもあります。
（１）
点対称であり線対称でもある模様で、図３以外のものを１つかきなさい。
（２）
点対称の模様は何通りできますか。ただし、図３と（１）でかいた模様もふくみます。
（３）
線対称の模様は何通りできますか。ただし、図３と（１）でかいた模様もふくみます。
＠解説＠
（１）
図３が点対称であり線対称でもある模様。
90°の回転は違う模様と考えるので、図３を90°回転させれば答えになる。
＠＠
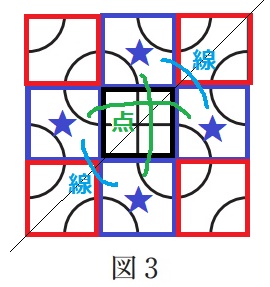
これ以外の正答はないと思われる。
点対称となるには中央に＋、＋を挟んだ反対側に同種の模様を置く必要がある。
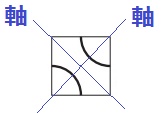
模様の対称の軸は縦・横ではなく、斜めしかない。９マスでも同様に軸は斜めになる。
点対称かつ線対称を満たすには４つの青マス（★）に同種の模様がくる。
（残りの赤マスに同種の模様）
青マスと赤マスにどちらの模様を置くかで２通りしかない。
（２）
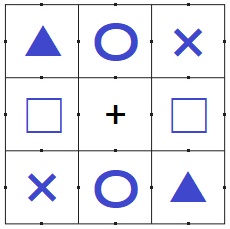
点対称なので中央が＋、＋を挟んだ両端に同種の模様がくる。
〇▲□×の４つから２つを選んで同種の模様を置く。
（残り２つは別の同じ模様が自動で置かれる）
４Ｃ２＝６通り
（３）
対称の軸は斜めしかない。
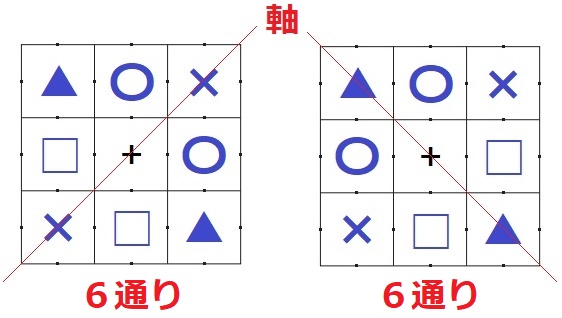
＋が中央にある場合。
軸に対して対応するマスに同種の模様を置く。
軸は右上と右下の２パターンで、おのおの４Ｃ２＝６通りずつある。
留意点は〇と□が同種のときに重複が発生すること！
（１）で★が同種のときは点対称かつ線対称になった。
〇と□の４マスが同種だと、残りの四隅は別の同種で互いに重複が発生。
これが２通りあるから、６＋６－２＝10通り
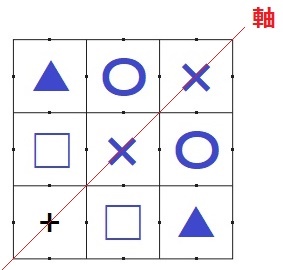
＋が四隅にあるときも線対称ができる。
４Ｃ２＝６通り
＋が別の隅にある場合を含めると、６×４＝24通り
（回転させると、軸上の＋××が回る→重複なし）
したがって、10＋24＝34通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント