平均50.5点(前年比;-3.4点)
最高点97点、最低点0点

出題範囲の削減は〔啓林館 未来へひろがる数学3〕194ページ以降。
大問1(小問集合)-77.3%
(1) 98.4%
-3-6
=-9
(2) 93.8%
-7/10×(-5/21)
=1/6
(3) 91.6%
1-(-3)2
=1-9
=-8
(4) 94.6%
-4(a-b)+5(a-2b)
=-4a+4b+5a-10b
=a-6b
(5) 80.7%
(√8+√18)÷√2 ←根号同士で割る
=√4+√9
=2+3
=5
(6) 85.9%
x2-10x=-21
x2-10x+21
=(x-3)(x-7)=0
x=3、7
(7) 59.8%
a>0だから、グラフは下に凸。
x=0のとき、最小値y=0
x=-2のとき、最大値y=4
0≦y≦4
(8) 53.3%
ア:15人の中央値は8番目の値だが、表では不明。×
イ:2年生の合計24×15は、3年生の合計25×15より小さい。〇
ウ:範囲(レンジ)=最大値-最小値。いずれも範囲は15。〇
エ:最頻値(モード)は最も多くあらわれている値。表では不明。×
イ、ウ
(9) 31.9%!
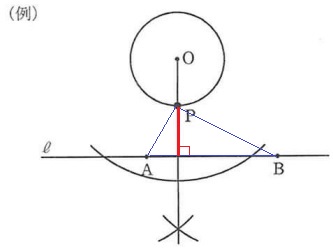
△ABPの面積を最小にする→Pと直線ℓの距離(△ABPの高さ)を短くする。
Oを通る直線ℓの垂線をひき、円周との交点がP。
大問2(確率・方程式)-51.9%
(1)① 44.8%
あくまでも確率なので絶対はない。
同様に確からしいとは、結果が同じように起こると期待できること。
ア『かならず』イ『少なくとも1回』『ちょうど』とは断言できない。
エ
② 75.1%
答案では説明も書く。
玉の取り出し方は、3×4=12通り
和が5になる組み合わせは、(1、4)(2、3)(3、2)の3通り。
確率は、3/12=1/4
(2)① 77.0%
6人なので団体割引はなし。
A~D間は660円、A~F間は1200円。
660×3+1200×3
=(660+1200)×3
=1860×3
=5580円
② 17.4%!
答案では過程も記述する。
1人あたりの通常運賃さえわかれば、表から何駅から何駅まで移動したかわかる。
そこで、1人あたりの通常運賃をx円とする。
団体割引が適用されるから、大人1人は0.7x円、中学生1人は0.5x円。
0.7x×5+0.5x×15=6600
11x=6600
x=600
『列車はA駅からF駅に向かって進む』
表より、通常運賃が600円となるのは、B駅で乗ってE駅に降りた。
乗った駅…B駅、降りた駅…E駅
大問3(関数)-40.5%
(1) 28.1%!
反比例の例を挙げる。
〔面積が18cm2である長方形の縦をxcm、横をycm〕とすると、
yはxに反比例する。
y=18/x
〔18kmの道のりを歩く速さを時速xkm、歩く時間をy時間〕とすると、
y=18/x
〔18mのリボンをx等分したとき、1本あたりの長さをym〕とすると、
y=18/x
(2)① 75.3%
反比例の比例定数aは積xyで一定。
Aの座標から、a=-2×6=-12
② 47.8%
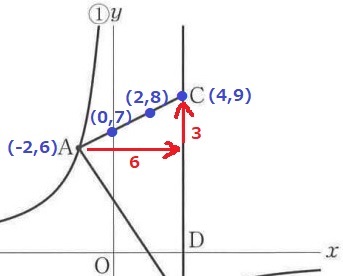
A(-2、6)⇒C(4、9)
右に6、上に3だから傾きは1/2
Aから右に2、上に1の移動で格子点を通過する。
4個
③ 10.8%!
y=-12/xにx=4を代入して、B(4、-3)
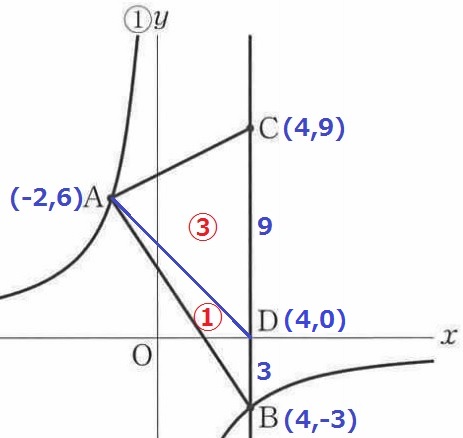
Dを通る△ABCを2等分する直線は、DからAC方面に向かうはず。
試しにADに補助線をひくと、BD:DC=3:9=1:3から、
△ABDの面積を①とすると、△ADCは③
△ABCは④だから、②ずつに配分すれば2等分になる。

△ADCを①と②に分割。
ACを1:2に内分する点をEとすると、△ADE=①、△EDC=②
直線EDで△ABCの面積が2等分される。
E座標は前問で判明している。4つの格子点の左から2番目である。
E(0、7)→D(4、0)
右に4、下に7だから、傾きは-7/4
切片はEのy座標7
y=-7/4x+7
大問4(平面図形)-31.9%
(1) 81.3%
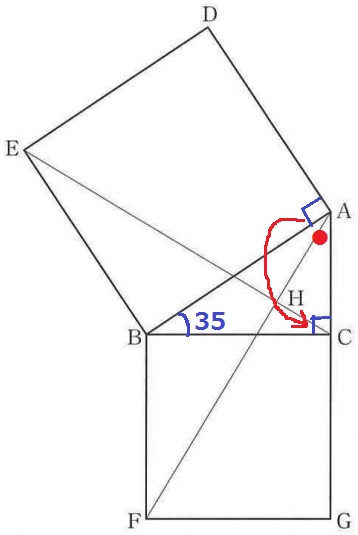
△ABCの内角で決着がつく。∠DAB=∠ACB=90°より、
∠DAG=∠DAB(90)+∠BAC(●)
=∠ACB(90)+∠BAC(●)
=180-35=145°
(2) 35.7%
△ABF≡△EBCの証明。
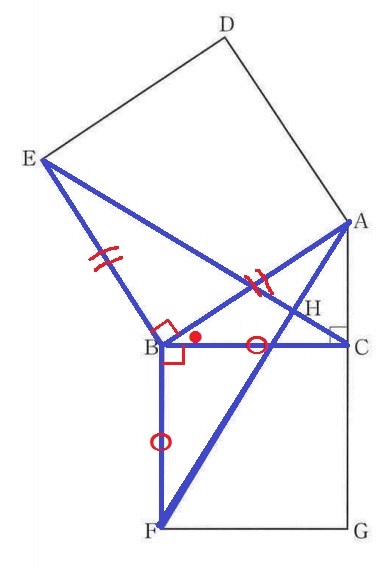
正方形の1辺で、AB=EB
同様に正方形の1辺で、BF=BC
∠ABF=90+●=∠EBC
2辺とあいだの角が等しいから合同。
@余談@
△ABFをBを回転の中心として反時計回りに回転移動すれば△EBC
(3)① 5.7%!!

△ABCの面積は、3×2÷2=3cm2
△ABCで三平方→AB=√13cmより、正方形ABEDは13cm2
五角形ACBEDは13+3=16cm2で、これから△EBCをひけば四角形ECADが求まる。
△EBCの底辺は3cm。高さをどうするか。。
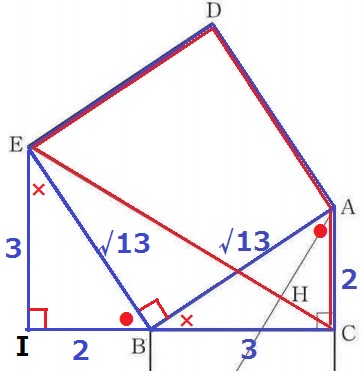
高さを作ってしまう。
CBの延長線とEからおろした垂線の交点をIとする。
●+×=90°で角度を調査すると2角が等しく、
正方形の1辺でAB=BEだから、1辺両端角相等で△ABC≡△BEI
△EBCの高さはEI=3cm。
求積すべき四角形ECADの面積は、16-3×3÷2=23/2cm2
@余談@
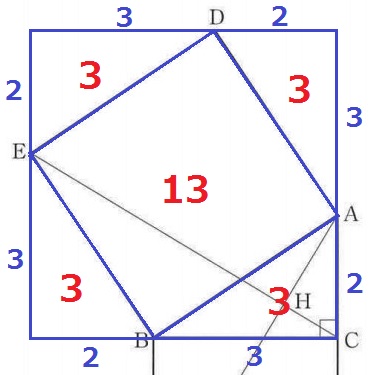
↑この形は三平方の定理の証明にもでてくる。
同じ直角三角形を一周してグルっと敷き詰めると、
中央の正方形ABEDの面積は、5×5-3×2÷2×4=13cm2
1辺は√13cmだから、22+32=(√13)2が成り立つ。
② 4.2%!!
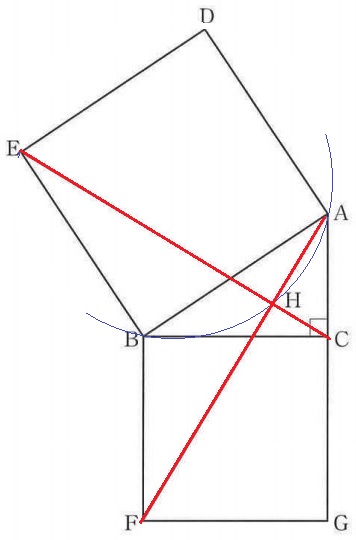
弧の長さを求めるので、円の中心を探す。
左上の方にありそう・・。
なんとなく、AFとECが直交しているように見える。
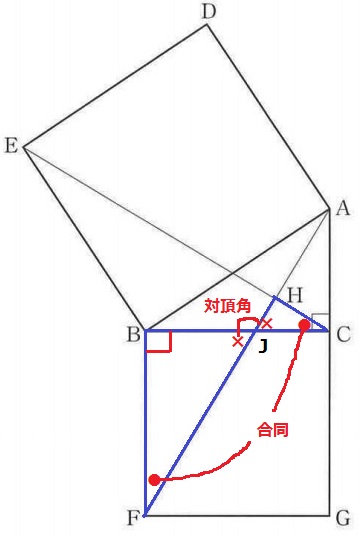
BCとAFの交点をJとする。
△BJFと△HJCにおいて●+×=90°で角度を調査すると、
対頂角(×)と合同の対応する角(●)で2角が等しく∽
∠JHC=∠JBF=90°だから、予想通りAFとECは直交していた。
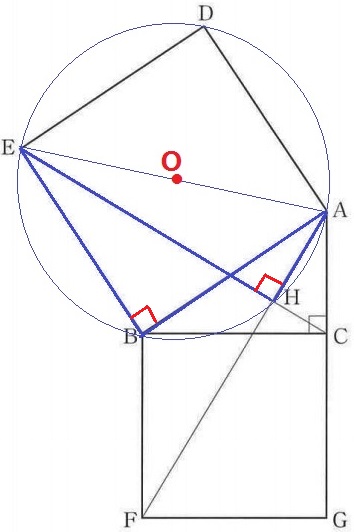
中心の探索は円周角定理の逆を使う。
AEについてBとHが同じ側にあって∠ABE=∠AHE=90°だから、
4点A・H・B・Eは同一円周上にある。
半円の弧に対する円周角は90°だから、円の直径はAEでこの中点が中心Oである。
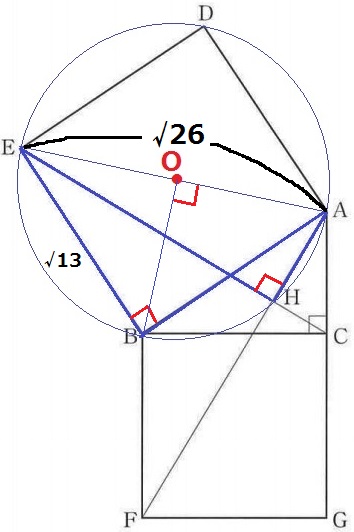
正方形の半分である△ABEは直角二等辺。
1:1:√2より、直径AE=√13×√2=√26cm
Hを含む弧ABの中心角は∠AOB=90°
√26×π×1/4=√26/4πcm
大問5(空間図形)-30.0%
(1) 80.5%
△ABCで三平方。
辺の比は3:4:5で、AC=10m
(2) 39.2%

ACとBDの交点をHとする。
Pから垂線をおろすと、その足はHにあたる。
HC=10÷2=5m
△PCHで三平方→5:12:13の直角三角形でPH=12m
正四角錐PーABCDの体積は、8×6×12÷3=192m3
(3)① 0.0%!!!
難しい。

四角錐の底面ABCDを45°傾けると台形ABEFに変わった。
45°が重要なキーになるので、まず、45°を図示したい。
そこで、四角錐を正面からみたときの様子を考える。
AB・CD・EFの中点をそれぞれQ・R・Sとすると、
△PQRは底面ABCDに対して垂直な面である。
長方形ABCDを台形ABEFに45°起き上がらせるとRQがSQになるから、
SQとRQがなす角度、すなわち、∠SQR=45°である。
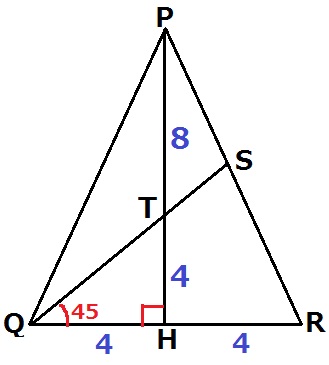
PHとQSの交点をTとする。
△THQは内角が45°ー45°ー90°で直角二等辺三角形。
TH=QH=4m
PT=12-4=8m
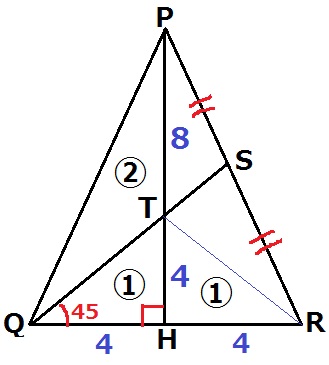
PHは中線(Pと対辺QRの中点を結んだ線)で、PT:TH=8:4=2:1だから、
Tは△PQRの重心である⇒重心を通過するQSも中線で、SはPRの中点。
重心を使いたくない人は、TRに補助線を引き、
△QPT:△QTH=②:①。QH:HR=1:1より△QTH=△RTH=①だから、
高さの比で、PS:SR=△QPT:△QRT=②:②=1:1と出ます。

SがPRの中点であることをふまえ、再び立体に戻る。
△PEF∽△PCDより、EF=6÷2=3m
SからQRに垂線、足をUとすると、UはHRの中点だからHU=2m
直角二等辺SUQより辺の比は1:1:√2だからQS=6√2m
これが台形ABEFの高さにあたる。
台形の面積は、(3+6)×6√2÷2=27√2m2
② 0.4%!!?
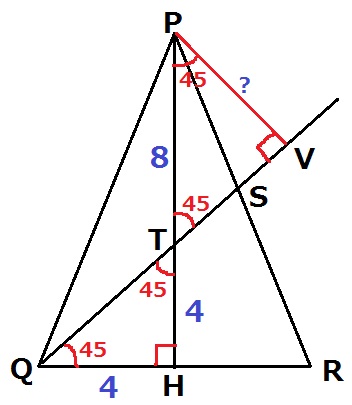
台形ABEFの面積を求めたので、これを底面としたときの高さがわかればいい。
QSを延長、Pからの垂線との交点をVをすると、PVが四角錐の高さにあたる。
対頂角で45°を移すと、△PVTは直角二等辺。
1:1:√2より、PV=8×1/√2=4√2m
したがって、四角錐P―ABEFの体積は、27√2×4√2÷3=72m3
@余談@

台形ABEFの面積を経由せず、△PQSの面積から体積を求めることもできる。
PS=SRより△PQSは△PQRの半分だから、8×12÷2÷2=24m2
四角錐PーABEFは△PQSを挟んで左右対称。
底面積を△PQSとみなして断頭三角柱の考えを使うと、
BA=6m、EF=3m、Pは0mだから、
高さの平均は(6+3+0)÷3=3m
24×3=72m3
テクニカルな解法ですが、このようなタイプの問題では断頭三角柱が光ります。
@@

甲陽学院で類題が出題されました。
難問ですが、余力のある方は挑戦してみてください。
●講評●
大問1
正答率は高い。
後半戦を考えるとここで失点したくない。
(9)底辺ABの長さが固定なので、高さを最小にする。
大問2
(1)①もう少し正答率があって良いと思うが。
(2)②何を文字におくべきか。表では300と480以外は数値がバラけている。
通常運賃をxとおけば、団体割引が適用された運賃もxで表せる。
大問3
(1)反比例の具体例をあげる。よく経験してきたと思うが正答率は悪かった。
他には、歯車の歯数と回転数の関係が挙げられる。
(2)③いろんなやり方がある。解説では①:③→②:②にして二等分線を見つけた。
大問4
(2)頻出の証明。
(3)①合同の直角三角形をくっつける発想はどこかで経験しておきたい。
②中心点は円周角定理の逆をよぎらせる。90°があれば直径が見つかる。
なんとなく垂直っぽいという着眼は大事。あとで検証する。
大問5
(3)①難問。45°をどの平面で記述するか。
台形ABEFと長方形ABCDを2等分する面に目をつける。
また、四角錐全体を正面からみた図だと、面の移動がつかみやすい。
SはPRのちょうど真ん中にくる。
②なぜ0.0%から0.4%に上がったのか??


コメント