2022年度　ラ・サール中学過去問【算数】大問４解説

問題ＰＤＦ
たて４ｃｍ、横６ｃｍの長方形を図のように１辺の長さが１ｃｍの正方形24個に区切ります。
そして、点Ａから点Ｂへ至る最短経路で長方形の面積を２等分することを考えます。
図の太線はその１例です。次の問に答えなさい。

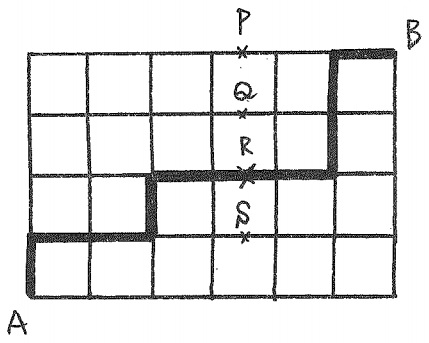
（１）
点Ｐを通るものと、点Ｓを通るものはそれぞれ１通りです。
それらを解答用紙に書きなさい。

（２）
点Ｑを通るものは何通りありますか。

（３）
全部で何通りありますか。

＠解説＠
（１）
１通りしかないとあるので、頑張って探す。

24マスの半分だから、12マスずつに分ければいい。

（２）

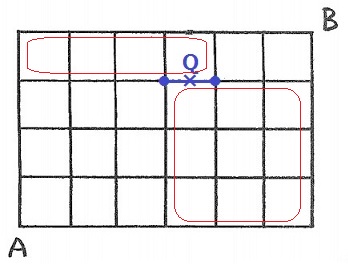
イメージすると、２つの枠は必ず分離される。
右下が９マスなので、あと３マス追加すれば12マスで全体が２等分される。

右上の３ルートで場合分け。
右上２マスを右下９マスにくっつけると、左下は１マス→１通り
右上１マスでは左下２マス→２通り
右上０マスでは左下３マス→３通り
高さを調整する感じで数えよう。
計６通り。

（３）

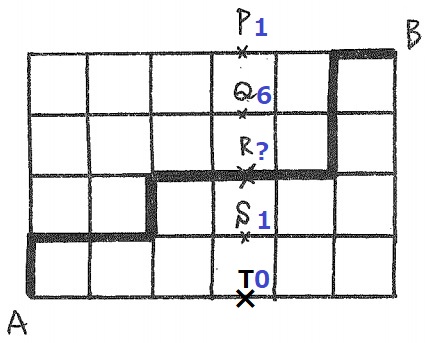
Ｓの下をＴとする。
ＡからＢまで行くには、必ずＰ～Ｔのいずれか１つを通過する。
Ｔを試すと２等分にできない⇒０通り
あとはＲだけ調べればいい。

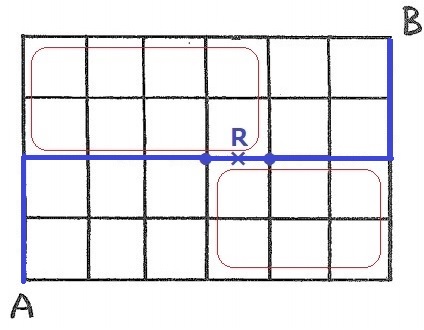
右上が４マスしかない。
これと左上８マスがどうくっつかで場合分けする。
４マスくっつくと１通り。

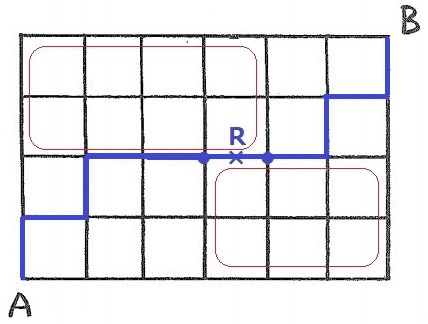
３マスくっつけると、左下で１マス追加する。１通り

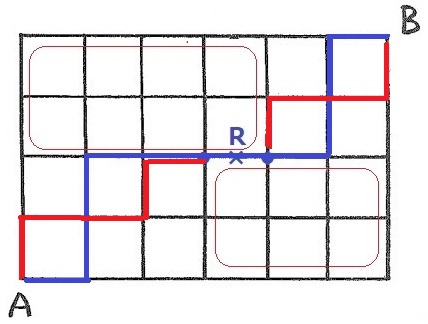
２マスくっつける。左下で２マスくっつける。２×２＝４通り

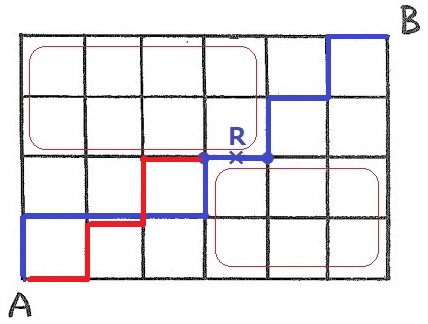
１マスくっつける。左下は３マスで２通り。

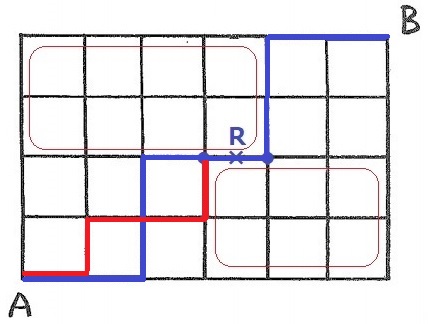
左下だけで４マスくっつける。２通り
Ｒは合計10通り。
よって、１＋６＋10＋１＝18通り
難関中（算数科）解説ページに戻る