問題ＰＤＦ
Ａ、Ｂ２つの皿と、３ｇ、４ｇ、５ｇ、６ｇ、７ｇ、８ｇ、９ｇの７つの分銅があり、
９ｇの分銅はＡにのせてあります。残りの６個の分銅もＡ、Ｂどちらかの皿にのせます。
ただし、Ｂには少なくとも１個の分銅をのせるものとし、皿の重さは考えません。
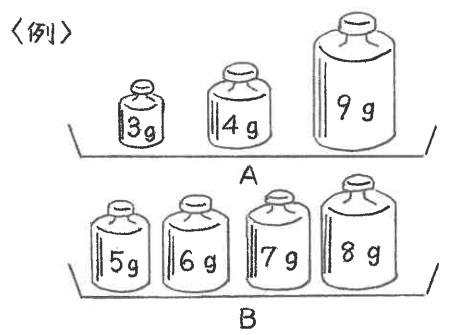
＜例＞のようなのせ方をしたとき、Ａだけに着目して〔３４９〕と表すことにします。
そのとき、数字は小さい順に書きます。次の各問に答えなさい。
（１）
Ａ、Ｂの重さが等しくなるようなのせ方をすべて書きなさい。
ただし、〔３４９〕のように、Ａだけに着目した表し方をしなさい。
（２）
ＢがＡより重くなるのせ方は全部で何通りありますか。
（３）
ＡがＢより重くなるのせ方は全部で何通りありますか。
＠解説＠
（１）
３ｇ～９ｇの和は42ｇ。
42÷２＝21ｇずつＡとＢに配分すればいい。
Ａに21－９＝12ｇを追加でのせる。
12＝４＋８＝５＋７
８を３＋５に分解して、３＋４＋５にできる。
７を３＋４に分解できるが、３＋４＋５で前と同じ。
〔４８９〕〔５７９〕〔３４５９〕
（２）
Ａに12ｇ追加で釣り合うから、Ａの追加分が11ｇ以下になればＢが重くなる。
Ａに追加するおもりの個数で場合分け。
●Ａに追加なし
分銅すべてをＢに乗せる。１通り
●Ａに１個追加
３ｇ～８ｇすべてＯＫ。６通り
●Ａに２個追加
３ｇと４～８ｇ→５通り
４ｇと５～７ｇ→３通り
５ｇと６ｇ→１通り
●Ａに３個追加
３＋４＋５＝12ｇなので無し。
よって、16通り。
（３）
３～８ｇの６個をＡかＢに乗せる。
２×２×２×２×２×２＝64通り
注意点は『Ｂには少なくとも１個の分銅をのせる』ので、
全体のパターンは分銅すべてをＢにのせる場合をのぞいた63通り。
（１）がＡ＝Ｂ、（２）がＡ＜Ｂだから、余事象でＡ＞Ｂが求まる。
63－（３＋16）＝44通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント