平均46.55点（前年比；＋6.86点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）① 88.2％
４－（－９）
＝４＋９
＝13
② 78.6％
√６×√３－√８
＝３√２－２√２
＝√２
③ 69.1％
６ａ3ｂ×ｂ/３÷２ａ
＝ａ2ｂ2
④ 65.5％
（ｘ＋６ｙ）/３＋（３ｘ－４ｙ）/２
＝｛２（ｘ＋６ｙ）＋３（３ｘ－４ｙ）｝/６
＝（２ｘ＋12ｙ＋９ｘ－12ｙ）/６
＝11/６ｘ
（２） 40.9％
（ｘ＋３）（ｘ－７）＋21＝０
ｘ2－４ｘ－21＋21
＝ｘ2－４ｘ
＝ｘ（ｘ－４）＝０
ｘ＝０、４
大問２（小問集合）
（１） 64.1％
ｘ＝－６、ｙ＝１を代入。
－６ａ＋ｂ＝－11 …①
－ａ－６ｂ＝－８ …②
①－②×６をすると、37ｂ＝37
ｂ＝１
①に代入して、ａ＝２
ａ＝２、ｂ＝１
（２） 43.6％
１枚目のカードは元に戻す。
全体は６×６＝36通り
反比例ｙ＝６/ｘ→ｘｙ＝６
（ａ、ｂ）＝（－３、－２）（－２、－３）（２、３）（３、２）の４通り。
確率は、４/36＝１/９
（３） 40.5％
ワイシャツの定価をｘとすると、その３割引きは0.7ｘ。
0.7ｘを３着、ｘを２着買うから、
0.7ｘ×３＋２ｘ
＝4.1ｘ＝8200
ｘ＝2000
ワイシャツ１着の定価は2000円。
（４） 43.2％
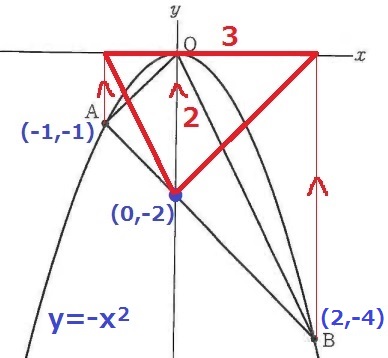
Ａ（－１、－１）⇒Ｂ（２、－４）
右に３、下に３だから傾きは－１。
Ａから右に１、下に１移動して切片は（０、－２）
△ＯＡＢは幅３高さ２だから、３×２÷２＝３ｃｍ2
大問３（平面図形）
（１） 66.8％
△ＤＰＣ∽△ＤＱＲの証明。
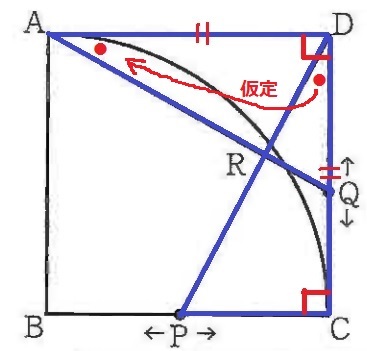
問題文では、まず合同を指摘している。
仮定と正方形１辺、90°をもとに１辺両端角が等しく、△ＤＰＣ≡△ＡＱＤ
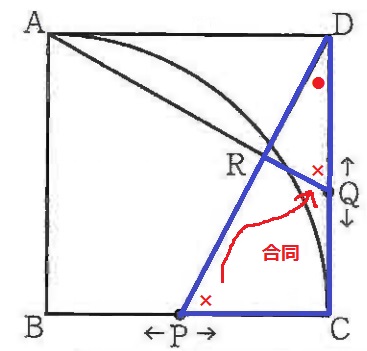
対応する角より、∠ＤＰＣ＝∠ＤＱＲ
共通角で、∠ＰＤＣ＝∠ＱＤＲ
２角相等で∽。
ａ…ア、ｂ…ウ、ｃ…エ
（２） 30.9％！
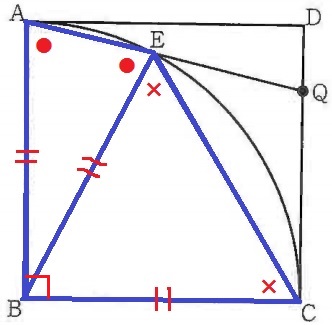
ＢＥに補助線。
半径より、△ＡＢＥと△ＥＢＣは二等辺三角形。
四角形ＡＢＣＥの内角から∠ＡＥＣ（●×）を算出する。
∠ＡＥＣ＝（360－90）÷２＝135°
（３） 15.0％！
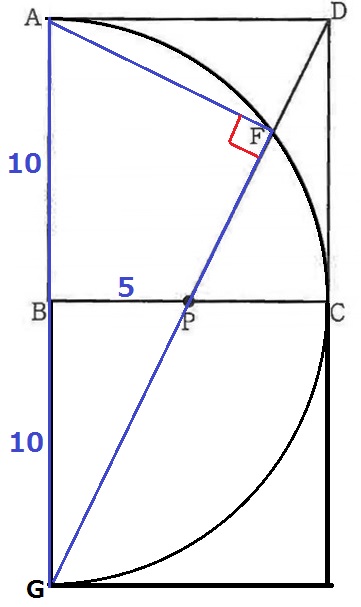
下に同じものを足すと半円になる。
Ｂの下をＧとすると、半円の弧に対する円周角ＡＦＧ＝90°
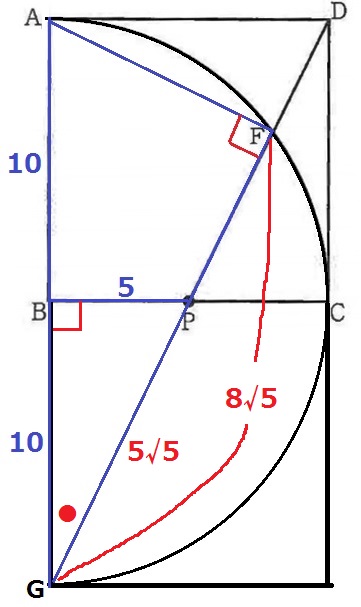
△ＰＧＢで三平方→ＰＧ＝５√５ｃｍ
△ＰＧＢ∽△ＡＧＦより、相似比はＰＧ：ＡＧ＝５√５：20＝√５：４
ＦＧ＝10×４/√５＝８√５ｃｍ
ＰＦ＝８√５－５√５＝３√５ｃｍ
大問４（数量変化）
（１）① 76.4％
バスＰが２回目のＢに着くには、片道３回分走る。
９×３＝27分
午前10時27分
② 54.5％
算数で解けるので、とりこぼしたくない。
バスＱは27分後にＰと同時にＢを出発する。
バスＱは27－７＝20分にＢへ着く。
ＡＢ間を20分で走るから、2700÷20＝分速135ｍ
（２） 7.3％!!
８分の位置を正確に図示する。
バスＱがＡに向かうのでグラフの後半。
その８分後にバスＰがＡに向かうから、グラフの最後の方の話である。
あとは三角形の相似でケリがつく。
バスＰは往復で18分。
うえの青い三角形の相似に着目すると、相似比は18：８＝⑨：④
ＡＢ間を⑨とすると、ＡＣ間が④、ＣＢ間が⑤となる。
したがって、ＣＢ間の距離は、2700×⑤/⑨＝1500ｍ
大問５（データの活用）
（１）① 50.5％
（０×１＋１×２＋２×１＋３×２＋４×２＋５×４＋６×３＋７×１＋８×３＋9×１）÷20
＝96÷20＝4.8冊
② 64.5％
最小値０冊、最大値９冊→最大値10冊のウが外れる。
20人の中央値（第２四分位数）は10番目と11番目の平均で５冊。
第１四分位数は下位グループ10個の真ん中（５番目と６番目の平均）で３冊。
イ
（２） 13.2％！
①四分位範囲＝第３四分位数（Ｑ3）－第１四分位数（Ｑ1）。Ｃの方が箱が長い。×
②中央値は第２四分位数（Ｑ2）で同じ。〇
③20人のQ1は５番目と６番目の平均。Q1が３冊のＣでも３冊以下は５人いる。〇
④平均値は×印などで示すが、本問の箱ひげ図には描かれていない。△
①…イ、②…ア、③…ア、④…ウ
大問６（空間図形）
（１） 45.9％
高さの数値が与えられている。
２×２×π×４√２÷３＝16√２/３πｃｍ3
（２） 31.4％！
側面積の扇形の中心角は〔×半径/母線〕なので、
側面積＝母線×母線×π×半径/母線＝母線×半径×π
２×２×π＋６×２×π＝16πｃｍ2
（３） 0.5％!!!
意地悪な設問< `∀´ >
最短距離の問題だが、ＯＡ上のＰはＯＰ＝２ｃｍで固定される一方で、
ＯＢ上のＱは『動く点』となっている。
ＢＰＱは一直線にあらず。
ＰとＯＢ’の最短距離は垂線。
ＰＱは折れ曲がり、ＱはＰを通る垂線の足になります(ﾟДﾟ)…
扇形の中心角は、360×３/６＝120°
Ａは弧ＢＢ’の中点なので、ＯＡは∠ＢＯＢ’の二等分線である。
∠ＢＯＡ＝∠Ｂ’ＯＡ＝60°
△ＯＰＱは内角が30°—60°—90°で辺の比が１：２：√３だから、ＰＱ＝√３ｃｍ
これと合同の直角三角形ＯＰＲを左側に作る。
ＰＲ＝√３ｃｍ、ＯＲ＝１ｃｍ
ＲＢ＝６－１＝５ｃｍ
△ＰＢＲで三平方→ＢＰ＝２√７ｃｍ
したがって、ひもの長さ（ＢＰ＋ＰＱ）＝２√７＋√３ｃｍ
記述問題の激減で教育関係者や受検生に驚きが広がったらしい…。
＞朝日新聞
大問１
20点とりたい。
大問２
（１）係数がいやらしかった。
（２）反比例→積が６で一定。
（３）割引券を３枚使う⇒0.7ｘ円が３着、ｘ円が２着を読み取る。
（４）典型題。
大問３
（１）対応する角と相似条件を選ぶだけ。
（２）円の中心とどこかを結ぶと解決策が見えてくる。
（３）王道の解き方ではないかもしれないが、ＰがＢＣの中点にあることに着目し、
ＢＣの下の世界をつくると半円の弧に対する円周角があらわれる。
大問４
（１）算数レベル。
（２）８分の位置はＱ→Ｐの順で探る。
大問５
（２）本問の箱ひげ図では平均がわからない、という選択肢はいろいろな場所で見かけました。
大問６
（２）までは基本。
（３）性悪だった(´・_・`)
本来、直線になるべきヒモを強引に折り曲がらせるには、Ｐに釘を打つ必要があるのでは？
物理的にピーンと張れないのにヒモを持ってきたのはどうなんでしょうか(´･_･`)
公立高校入試解説ページに戻る
コメント
こんばんは。いつもお世話になっております。今日は、2022茨城県の公立高校数学入試問題の大問3(２)の「別解」についてお話ししたいと思います。
最初は、サボ先生のように補助線を引いて二等辺三角形を作り、∠AECを求めました。このあと、この問題は、円周角の定理に気づくと解けると思い、次のように解いてみました。
[別解］円周角の定理(１つの弧に対する円周角は、その弧に対する中心角の半分である。）より、点Bを円の中心として、半径ABの円を描くと、
∠AEC(円周角)=1/２∠ABC(中心角)
=1/２✕270°
=135° 答え 135°
以上ですが、 このように今回は、2通りの解法で解きましたが、実際の正答率は、30.9%でしたが、やはり正答率は5割以上になることを期待したい問題でもある。もしかしますと、サボ先生も今回の私の別解もご存知かもしれません。先生のご教示もいただけますと嬉しく思います。
サボ先生のブログの入試問題の解説は、とても分かりやすく説得力があり、受中生にとって、とても参考になる素晴らしい解法かと思います。そして、別解も検討してもらえますので、投稿者として、とても嬉しく思います。これからも身体に気をつけて、頑張ってください。家庭教師のお仕事もご精進ください。お助けマンより。
円周角でも解けますね。素晴らしい考えだと思います。
すみませんが現在プライベートの方で諸事情を抱えておりまして、
ブログの作業は少しずつ続けてまいりますが、これ以降の返信につきましては控えさせて頂きます。
申し訳ございません。