問題ＰＤＦ
２つの四角柱の水そうＡ、Ｂがあります。
水そうＡの深さは30ｃｍで、最初に深さ６ｃｍまで水が入っています。
水そうＢは深さが40ｃｍで水は入っていません。
まずＢに水を入れ始め、その５分後にＡにもＢに入れる水と毎分同じ量の水を入れ始めます。
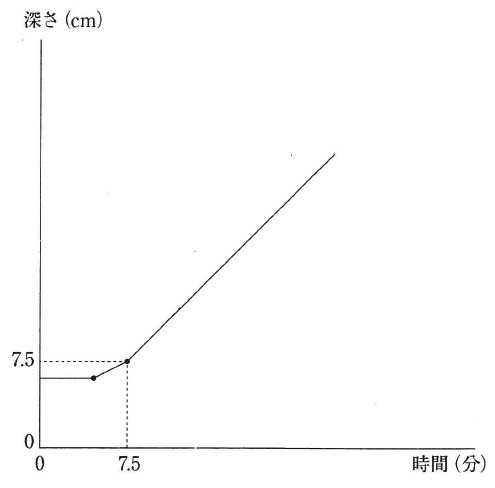
下のグラフはＢに水を入れ始めてからの時間と、Ａ、Ｂにたまる水の深さのうち
深いほうの深さのようすを途中まで表したものです。
このとき、次の各問いに答えなさい。
（１）
水そうＡの底面積は水そうＢの底面積の何倍ですか。
（２）
このまま水そうＡ、Ｂに入れ続けると、片方の水そうが水でいっぱいになったとき、
もう一方の水そうは水でいっぱいにはなりません。
そこで途中から一方の水そうに入れる水の量をそれまでと比べて毎分２倍にします。
すると、２つの水そうが同時に水でいっぱいになりました。
毎分２倍の量で水を入れたのはどちらの水そうで、何分間ですか。
＠解説＠
（１）
グラフのはじめは水深６ｃｍのＡだが、その後は２通りのシナリオが考えられる。
５分後、Ａに水が入り、7.5分後にＢがＡを追い越したか。
５分前にＢがＡを追い越し、7.5分後にＡがＢを追い越したか。
注目すべきは『Ｂに入れる水の量は０分から一定である』こと！
つまり、Ｂのグラフを描いたら原点０を通るはず。
ここから、グラフはＡ→Ａ→Ｂとなる。
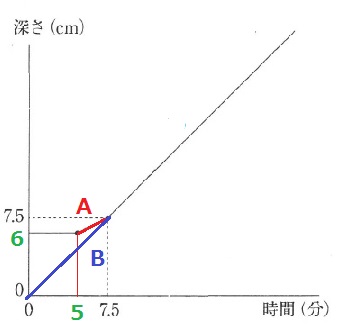
Ａ：2.5分間で水深1.5ｃｍ増→１分あたり、1.5÷2.5＝３/５ｃｍ増
Ｂ：7.5分間で水深7.5ｃｍ増→１分あたり、7.5÷7.5＝１ｃｍ増
ＡとＢの底面積は逆比（水深の増加速度が速いＢの方が底面積が小さい）。
Ａ：Ｂ＝１：３/５：１＝５：３
よって、Ａの底面積はＢの５/３倍。
（２）
Ｂがいち早く満水になる。
Ｂの深さは40ｃｍなので、40分後にＢが満水。
→Ａも40分後に満水となるよう仕向ける。
Ａは最初の５分間は水を入れず、水深６ｃｍからスタートなので、
『35分間で水深が24ｃｍ増加』すればいい。
あとは御馴染みの鶴亀算。
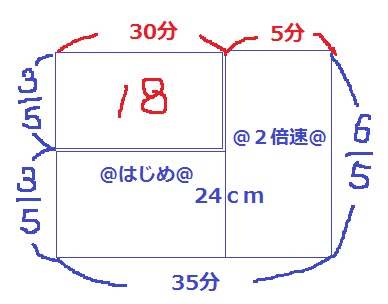
横が時間、縦が水深の増加速度、面積が水深の長さ。
左上の長方形が、35×６/５－24＝18
18÷（６/５－３/５）＝30分
２倍速でいれた時間は、35－30＝５分間
答えは、『水そうＡに５分間』
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント