2021年度　海城中学過去問【算数】大問６解説

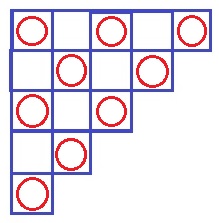
すべての面が白色の立方体と、すべての面が黒色の立方体がたくさんあり、いずれも１辺が１ｃｍです。これらを使って下の図のように立体を作ります。ただし、同じ段には同じ色の立方体が使われているものとします。例えば、３番目にできる立体は、上から１段目が１個の白色の立方体、上から２段目が３個の黒色の立方体、上から３段目が６個の白色の立方体でできています。

（１）
６番目にできる立体の表面のうち、黒い部分の面積を求めなさい。

（２）
６番目にできる立体の表面のうち、白い部分の面積を求めなさい。

（３）
〔　　〕番目にできる立体の表面のうち白い部分をすべて黒い色に塗った後、
この立体をばらばらにしました。このとき白く残った部分の面積の合計は720ｃｍ²でした。
〔　　〕にあてはまる数を求めなさい。

＠解説＠

６番目ということは一番下が黒。
下の面を考えなくていい、白の表面積が計算しやすい。
そこで、（２）から求める。

（２）

５番目の立体の図を手掛かりに、横から見たときの白は１＋３＋５＝９ｃｍ²
（連続する奇数の和の出し方；５が３番目の奇数だから３×３＝９ｃｍ²）
これが側面の４方向あるので、９×４＝36ｃｍ²

上からみたときもちょうど９面！
白の面積は36＋９＝45ｃｍ²

（１）
黒は全体の表面積から白45ｃｍ²を引けばいい。

↑６番目の立体は、６方向すべてこう見える。
１～６の和＝21
全体の表面積…21×６＝126ｃｍ²
黒の表面積…126－45＝81ｃｍ²

（３）
白の表面をすべて黒に塗り替える。
白く残った部分は、白の立方体の中の面である。

方針としては、【白の立方体の個数×６面＝黒に塗られる前の白の面積の合計
これから〔　〕番目の白の表面積を引くと中の合計が720ｃｍ²となる〔　〕番目を求める】

白の立方体は奇数番目で追加される。
１番目…１個
３番目…１＋（１～３の和）＝１＋６＝７個
５番目…７＋（１～５の和）＝７＋15＝22個
７番目…22＋（１～７の和）＝22＋28＝50個
９番目…50＋（１～９の和）＝50＋45＝95個
11番目…95＋（１～11の和）＝95＋66＝161個

白の面積の合計は、95×６＝570ｃｍ²、161×６＝966ｃｍ²
11番目から720ｃｍ²を超える。
とりあえず、11番目の白く残った部分を計算してみる。

（２）のように計算すると楽なので、一番下を黒の段にする→12段目で計算。
横から見ると、１＋３＋５＋７＋９＋11＝６×６（11は６番目の奇数）＝36ｃｍ²
これが４方向あり、上から見た白も同じ面積だから、白の表面積は36×５＝180ｃｍ²
白く残った部分は、966－180＝786ｃｍ²

720ｃｍ²を超えている。
12段目の黒を取っ払って11段にする。
底面にできる白の面積は１～11の和→66ｃｍ²
これが表面にむき出しになって黒に塗り替わったとすると、786－66＝720ｃｍ²
したがって、11番目。
難関中（算数科）解説ページに戻る