問題PDF
2つの建物A、Dと2つの壁B、Cが10mの等間隔で一直線上に並んでいて、図1のようにそれぞれの建物の端にはエレベーターがついています。建物Aのエレベーターは秒速1mで動き、建物Dのエレベーターは秒速2mで動きます。
また、図1のようにそれぞれの建物の屋上の高さは、建物Aは24m、建物Dは32mであり、また、壁Cの高さは12mです。なお、壁の厚さは考えないこととします。

今、建物Aのエレベーターが地上から屋上に向かって、建物Dのエレベーターが屋上から地上に向かって同時に出発しました。エレーベーターは地上または屋上に着くと、8秒間止まってから折り返して動き出すという動きを繰り返すこととします。
エレベーターは大きさを無視して床の面の高さで考えることにします。
(1)
エレベーターが動き始めてからの2分間で2つのエレベーターが同じ高さになることは
何回ありますか。ただし2台とも地上にある場合は除いて考えます。
(2)
A、Dのエレベーターと壁Cの上端の3つが初めて一直線上に並ぶのは、
エレベーターが動き始めてから何秒後ですか。
エレベーターにはカメラが取り付けてあり、外の様子を見ることができます。
カメラの取り付け位置は床と同じ高さの所です。
(3)
BとCの間の地面のうち、エレベーターが動いても壁に邪魔されてAとDのどちらのエレベーターのカメラからも見えない部分が2mあることが分かりました。このとき壁Bの高さを求めなさい。
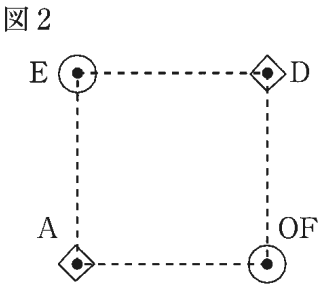
真上から見ると図2のように、高さ14mの塔OF(塔の上端がF、地上の点がO)、建物Aのエレベーター、高さ28mの塔E、建物Dのエレベーターは正方形の頂点上にあります。
このような配置のとき、塔OFの地上の点O、Aのエレベーター、Dのエレベーター、塔Eの上端の4点は空間内で平行四辺形の頂点になることがあります。
(4)
4点が初めて平行四辺形の頂点になるのはエレベーターが動き始めてから何秒後ですか。
また、2回目に平行四辺形の頂点になるのはエレベーターが動き始めてから何秒後ですか。
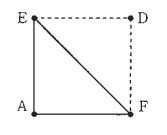
エレベーターが動き始めて21秒後にはAのエレベーターは地上21mの位置にあります。このとき、Aのエレベーター、塔Eの上端、塔OFの上端の点Fの3点でできる三角形を三角形AEFとします。
(5)
三角形AEFの各辺をのばした直線がそれぞれ地面と交わる3点は、
一直線上にあることを説明しなさい。
@解説@
(1)
ダイヤグラムを描いて調べる。
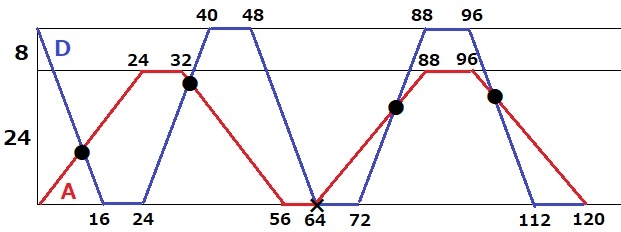
条件がやらしい。Aは24mを秒速1mで、Dは32mを秒速2mで往復する。
端についたら8秒間休む。2台とも地上にある場合を除くので、64秒後を除外すると4回。
(2)
A・C・Dが一直線になる場合を考える。

水平方向の2:1に着目する。
壁CとエレベーターDは平行。
もし、AC:CD=2:1であれば、上の2つの直角三角形は相似で一直線になる。
(後述の通り0秒後にADを2:1に分かつ点は12を超えるので、ADは右下の線にはならない)

垂直方向に整理するとこのようになる。
AC:CD=②:①となるのは何秒後か?

AとDが動いた距離は①、②とする。
③+③=32 ←÷3
①+①=32/3
①+②=12から上の式をひくと、①=12-32/3=4/3
①=32/3-4/3=28/3m
Aは秒速1mだから28/3秒後。
@別解@
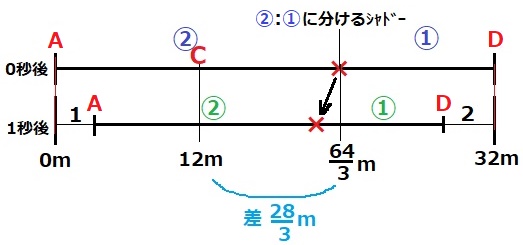
時計算に出てくるシャドーを用いる。
最初にADを2:1に分けるシャドーは、32×2/3=64/3m
このシャドーはAとDの動きに連動して常にADを2:1に分ける点で、
シャドーがCと一致したときが求めるべきAC:CD=2:1になる。
Cとシャドーは64/3-12=28/3m離れている。シャドーの速さが知りたい。
0秒後を②:①、1秒後を②:①とすると、
③=③+3→①=①+1
1秒後のシャドーは左に、(①+2)-①=(①+2)-(①+1)=1m移動している。
よって、シャドーがCに到着するのは28/3÷1=28/3秒後
@余談@
〇:〇に内分する点の位置がどう変化するか、条件を変えて調べてみました。
●1:1に内分する点
A1m/s+D1m/s→変化なし
A1m/s+D2m/s→左に1/2m/s
A1m/s+D3m/s→左に1m/s
A1m/s+D4m/s→左に1.5m/s
A1m/s+D5m/s→左に2m/s
*左に1/2mずつ移動。文字式で表すと、D-1/2(A+D)=1/2D-1/2A
●2:1に内分する点
A1m/s+D1m/s→左に1/3m/s
A1m/s+D2m/s→左に1m/s
A1m/s+D3m/s→左に5/3m/s
A1m/s+D4m/s→左に7/3m/s
A1m/s+D5m/s→左に3m/s
*左に2/3ずつ移動。D-1/3(A+D)=2/3D-A/3
●3:1に内分する点
A1m/s+D1m/s→左に1/2m/s
A1m/s+D2m/s→左に5/4m/s
A1m/s+D3m/s→左に2m/s
A1m/s+D4m/s→左に11/4m/s
A1m/s+D5m/s→左に7/2m/s
*左に3/4ずつ移動。D-1/4(A+D)=3/4D-A/4
(3)
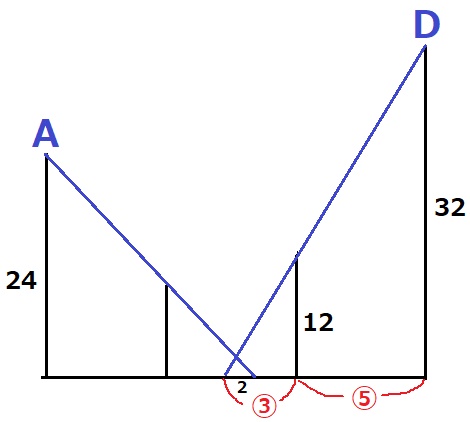
AとDから壁の上端を通るカメラの視線をひく。
あいだの2mが、いずれのカメラからも見えない領域。
右の三角形の相似比は、12:32=③:⑧(区間は⑤)
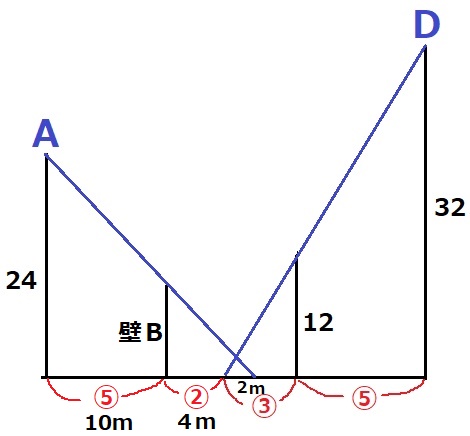
2mの左は⑤-③=②
⑤=10m→②=4m
壁Bの高さは、24×6/16=9m
(4)

E;28mと、O;0mは固定。AとDの高さが変わる。
最初に四角形AODEが平行四辺形になるのは、O~AとD~Eの高低差が等しいとき。
2秒後;D28m、A2m→4秒後に高低差4mで等しくなる。
(*計算で求めると、D②=A①+2m、①=2m→Aは4m移動→4秒後)
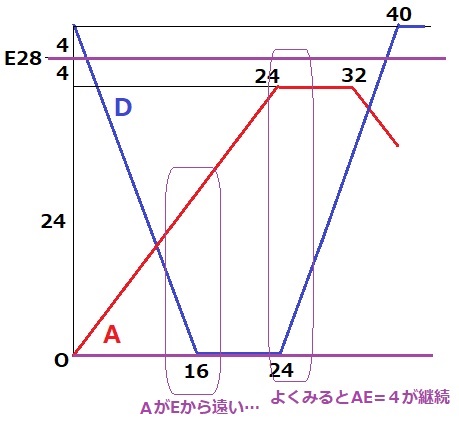
AとDの高さがすれ違い、16秒後にDはOにくるがAはEから遠い。
24秒後にAが到着、Dが出発するが、Aが休んでいる間はAE=4のままである!
Dが4cm移動した26秒後にO~DとA~Eの高低差が等しくなり、平行四辺形となる。
4秒後、26秒後
(5)

この3点が一直線上にあることを説明する。
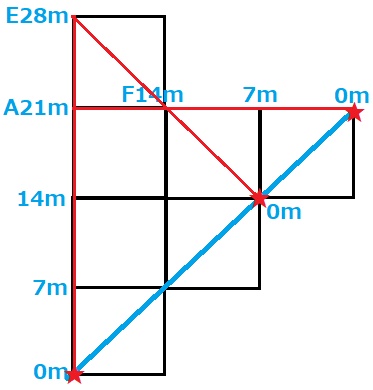
上から見た図で、高さ0mになるまでマスを描く。
3点は正方形の対角線上(一直線上)にある。



コメント