2020年度　洛南高等学校附属中学過去問【算数】大問２解説

問題ＰＤＦ
次の〔　ア　〕～〔　オ　〕にあてはまる数を答えなさい。

（１）
商品をある目標の数だけ作ります。
機械Ａでは１日に〔　ア　〕個ずつ作ることができ、ちょうど〔　ア　〕日でできあがります。
機械Ｂでは１日に（〔　ア　〕－３）個ずつ作ることができ、
（〔　ア　〕＋４）日でできあがります。

（２）
太郎君が初めいくらかのお金をもっていました。
１ヶ月あたり800円のおこづかいをもらい、
毎月〔　イ　〕円ずつ使うと９ヵ月後に残金は０円になります。
毎月〔　イ　〕円より200円ずつ多く使うと、６ヶ月後に残金は０円になります。

（３）
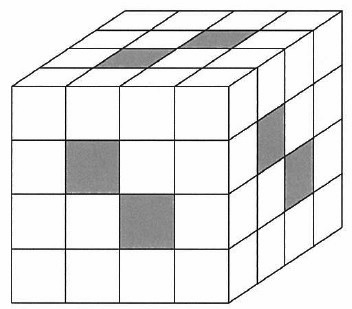
図のように、１辺の長さが１ｃｍの立方体を64個くっつけて、大きな立方体を作りました。
大きな立方体から、図の色が塗られている部分を反対側までくりぬきました。
このとき、残った立体の体積は〔　ウ　〕ｃｍ³となります。

（４）
図において、角うの大きさは〔　エ　〕度です。

（５）
図の色で塗られた部分の面積は〔　オ　〕ｃｍ²です。

＠解説＠
（１）
機械Ａは１日に●個を●日で作り上げるとする。

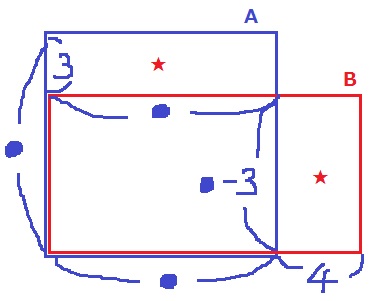
Ｂは１日に●－３個つくり、●＋４日かかる。
ＡとＢの四角形の面積が等しいので、★の面積も等しい。
●×３＝４×（●－３）
●×３＝●×４－12
●＝12
ア…12

（２）
基礎的なニュートン算。イ＝●円とする。

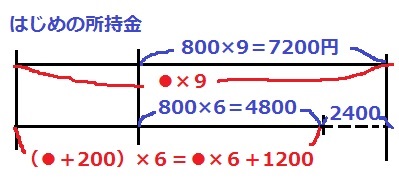
●×９＝●×６＋1200＋2400
●×３＝3600
●＝1200
イ…1200

（３）
１段ずつ検証していくのが確実。

１段目と４段目は14個ずつで28ｃｍ³
２段目と３段目は８個ずつで16ｃｍ³
28＋16＝44ｃｍ³
ウ…44

（４）

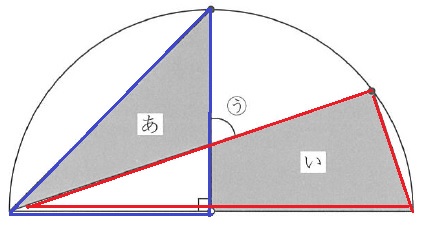
（あ）と（い）が同じ面積。
左下の白い部分を足すと、青い三角形と赤い三角形の面積が等しくなる。

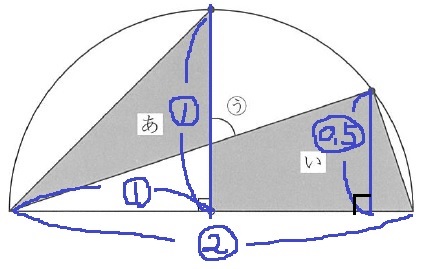
半径を①とおく。
三角形の面積比は〔底辺×高さ〕なので、
（い）を含む三角形の高さは、①×①÷②＝○0.5

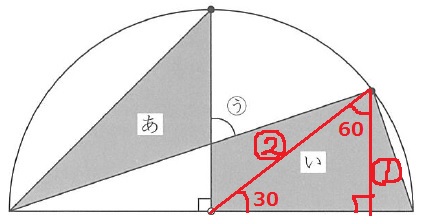
半径①：高さ○0.5＝②：①
ここから三角定規の30°－60°－90°の直角三角形がみつかる。

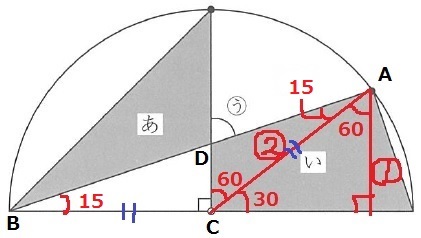
△ＡＢＣは半径から二等辺。外角定理より、∠ＢＡＣ＝30÷２＝15°
∠ＤＣＡ＝90－30＝60°
△ＡＣＤで外角定理→（う）＝15＋60＝75°
エ…75

（５）
発想が求められる。

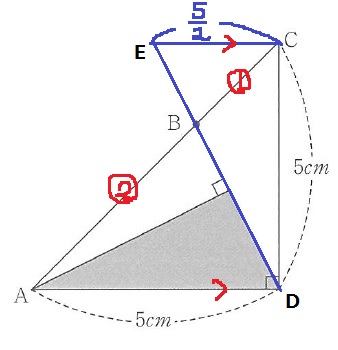
Ｃを通るＡＤに平行な線をひき、ＤＢの延長線との交点をＥとする。
△ＡＢＤと△ＣＢＥの相似から、ＡＢ：ＢＣ＝２：１
ＣＥ＝５×１/２＝５/２ｃｍ

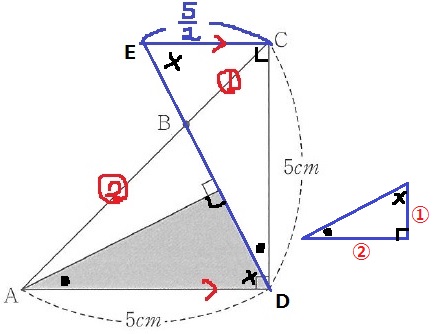
次に角度を調査していく。
色が塗られた三角形の内角を●－×－90°として調べると、
△ＣＤＥの内角も●－×－90°で、●－×－90°の直角三角形の辺の比は①：②とわかる。

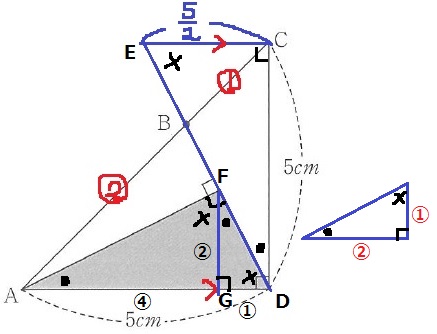
ＦからＡＤに向けて垂線をおろし、交点をＧとする。
△ＤＧＦと△ＦＧＡの内角も●－×－90°
ＤＧ＝①とすると、ＦＧ＝①×２＝②
ＡＧ＝②×２＝④
ＡＤ＝⑤より、ＦＧ＝５ｃｍ×②/⑤＝２ｃｍ
△ＡＤＦの面積は、５×２÷２＝５ｃｍ²
オ…５
難関中（算数科）解説ページに戻る