問題PDF
下の(例)のように、同じ整数を3回かけた数の答えは、連続する奇数の和で表すことが出来ます。
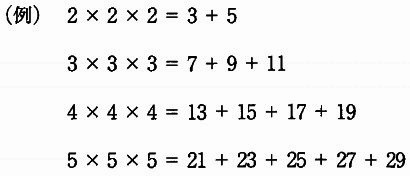
このとき、次の問いに答えなさい。
(1)
6×6×6を連続する奇数の和で表しなさい。
(2)
10×10×10を連続する奇数の和で表したとき、
その奇数の中で一番小さい奇数と一番大きい奇数の和を求めなさい。
(3)
(2×2×2)+(3×3×3)+(4×4×4)+…+(20×20×20)を求めなさい。
答えだけでなく、途中の計算や考え方も書きなさい。
@解説@
(1)
結果を観察して規則を探る。
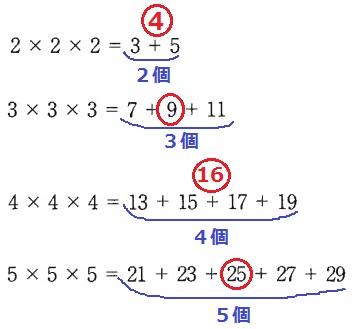
2×2×2は、真ん中が4で項の数は2個。
3×3×3は、真ん中が9で項の数は3個。
偶数だと項の数も偶数で、平方数の±1、±3…がペアで左右にあらわれる。
奇数だと項の数も奇数で、平方数を中央に平方数の±2、±4…がペアで左右にあらわれる。
6×6×6の項の数は6個。平方数36の±1、±3、±5が連なる。
6×6×6=31+33+35+37+39+41
(2)
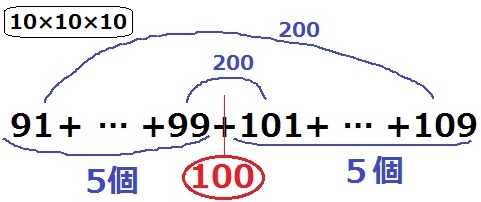
仕組みさえわかれば、すぐ解ける。
項の数は10個、左右に5個ずつのペアがあらわれる。
平方数100の±1、±3…±9となり、ペアの和は99+101=200
(3)
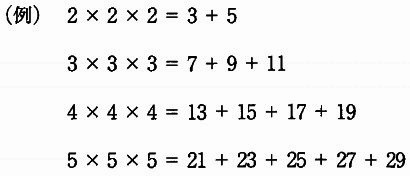
右辺の数字の並びをよく見ると、1を除く奇数が連続している。
ということは、20×20×20の最後の奇数までの和から1を引けばいい。

項の数は20個、左右で10個ずつ。
401を1番目とすると、10番目の奇数は419。
【1~N番目までの奇数の和→N×N】
e.g.)3は2番目の奇数→1+3=4=2×2
7は4番目の奇数→1+3+5+7=16=4×4
419は、(419+1)÷2=210番目の奇数
したがって、210×210-1=44099
@3乗和の公式@
1乗和の公式(1+2+・・・n)=n(n+1)/2
3乗和の公式(1×1×1+2×2×2+n×n×n)={n(n+1)/2}2
3乗和は1乗和の値を2回かけるだけで出せてしまう。
(ex.1~20までの3乗和の場合。1~20の1乗和が210だから、3乗和は210×210=44100)
これは幾何の発想で公式を導くことができます。詳しくはコチラ→ロボット・IT雑食日記

3乗和が1乗和の2乗。2乗なので正方形の面積で考える。
1×1×1が青の正方形。
2×2×2は2×2の正方形が2つあり、1つを半分にわけてくっつけると青+緑の正方形の面積になる。
3×3×3は3×3の正方形を3つくっつける(オレンジ)
4×4×4は4×4の正方形が4つあり、1つを半分にわけてくっつける(赤)
全体の正方形をみると、1辺が1の正方形、1+2の正方形、1+2+3の正方形、1+2+3+4の正方形…と広がっていくので、3乗和は1乗和の2乗となる。

浅野中学で2乗和が出ています。


コメント