問題PDF
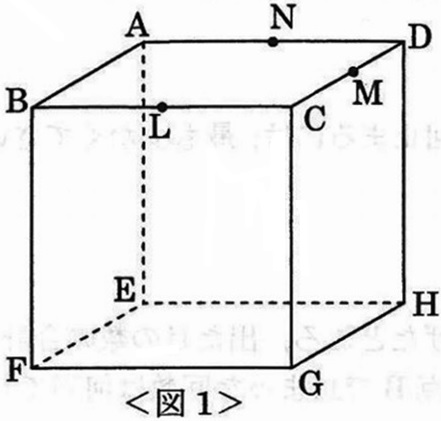
下の<図1>のように、1辺の長さが10cmの立方体ABCD-EFGHがあります。
辺BC、CD、DAの真ん中の点をそれぞれL、M、Nとするとき、次の各問いに答えなさい。
(1)
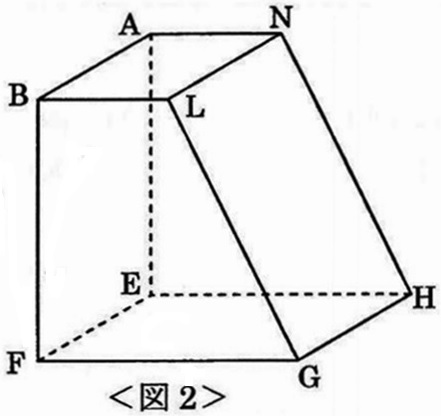
4点L、N、H、Gを通る平面で立方体ABCD-EFGHを切り、2つの立体に分けます。
<図2>は2つの立体のうち頂点Eを含む立体です。
その中に、はみ出ないようにできるだけ大きい立方体を、1つの頂点が点Eと重なるように置きます。
このとき、その立方体の1辺の長さを求めなさい。
(2)
3点L、M、Gを通る平面で立方体ABCD-EFGHを切り、2つの立体に分けます。
<図3>は2つの立体のうち頂点Eを含む立体です。
その中に、はみ出ないようにできるだけ大きい立方体を、1つの頂点が点Eと重なるように置きます。
このとき、その立方体の1辺の長さを求めなさい。

(3)
下の<図4>のように、辺AD、BC上にそれぞれ点P、Qを、DPとCQの長さが等しくなるようにとります。
3点Q,M、Gを通る平面と3点P、M、Hを通る平面で立方体ABCD-EFGHを切り、3つの立体に分けます。
その中に、はみ出ないようにできるだけ大きい立方体を、1つの辺が辺EFと重なるように置きます。
その立方体の1辺の長さが8cmであったとき、元の立方体のDPの長さを求めなさい。

@解説@
切断した立方体のなかに入る、最大の立方体の1辺を求める難問。
(1)

奥行きはフルで10cmなので、配慮すべきは縦と横の辺。
正面の台形BFGLからみて、その内部にできる正方形を考える。
直角三角形CGLの辺の比は、LC:CG=1:2
うえのような補助線をひき、直角三角形LPQは、LP:PQ=②:①
正方形の1辺OQ=①+5となる。
今度は縦方向で考えて、BF=BO+OF=②+(①+5)=③+5=10
①=5/3
正方形の1辺OQ=5+①=5+5/3=20/3cm
(2)
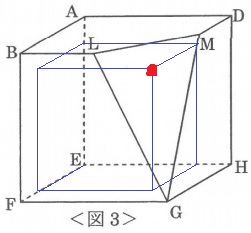
赤い頂点は△LMGのどこで接するか?
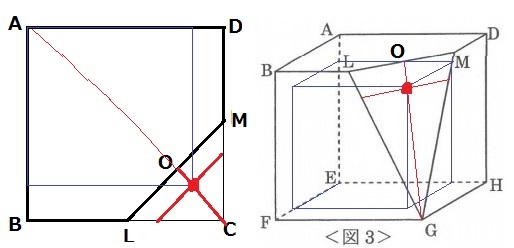
上からながめるとLMの外側に赤い頂点がくるが、
△LCMが直角二等辺三角形であることから、LMに平行な線分の中点を想像する。
LMの中点をOとすると、O-赤い頂点-Cのラインは正方形の対角線AC上にある。
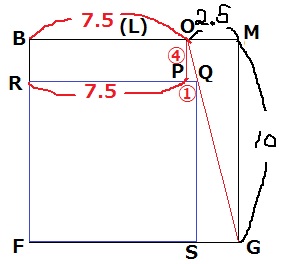
前問のように、正面から考える。
LO=OMより、OM=5÷2=2.5
BO=10-2.5=7.5
直角三角形OMGの辺の比OM:MG=2.5:10=1:4
△OPQにおいて、PQ:OP=①:④
正方形の1辺RQ=7.5+①だから、
BF=④+(7.5+①)=⑤+7.5=10
①=0.5
RQ=7.5+0.5=8cm
(3)
今度は正方形の1辺が8cmとわかっており、切断された辺の長さを求める。

△MQGと接する立方体の赤い頂点とGを通る直線をひく。
これとQMとの交点をOとして正面から見ると、先ほどと同じ構図になる。
辺の比が1:4の直角三角形→OM=2.5cm
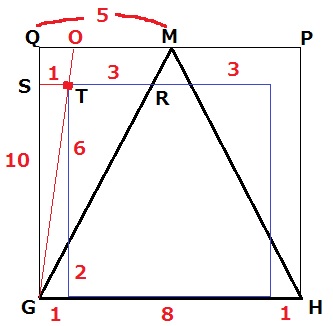
今度は側面(右)からみる。
左右対称なので、底辺GHは1:8:1の長さに分かれる。
直角三角形QMGの辺の比がQM:QG=1:2なので、
ここから他の直角三角形の長さを算出すると上図になる。
立方体の赤い頂点をTとし、Tを通るQMに平行な線をひき、QG、MGとの交点をS、Rとする。
注目すべきは、ST:TR=1:3
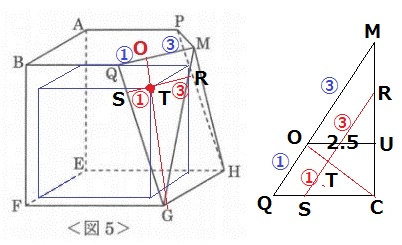
このS-T-Rラインを、立体図および上から見た図で示すとこうなる。
上からみた図で、Oを通るQCに平行な線をひき、MCとの交点をUとする。
はじめに正面からみた図でOM=2.5cmと出したのは、立体的に捉えなおすとOUにあたる。
△MOU∽△MQCより、QC=2.5×4/3=10/3
QC=DPより、DP=10/3cm



コメント