問題PDF
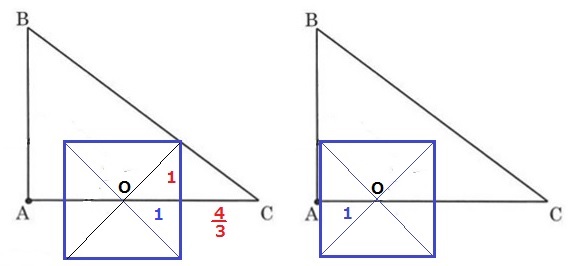
3辺の長さが3cm、4cm、5cmの直角三角形ABC(図1)と1辺の長さが2cmの正方形(図2)があります。正方形の対角線の交点を点Oとします。まず、図3のように点OがAと重なるように正方形をおきます。

この状態から正方形を、向きを保ったまま(回転することなく)動かします(図4)。点Oは、直角三角形の辺上をA→B→C→Aの順に毎秒1cmで動き、再びAに戻ってきたら止まります。
以下の問では、直角三角形と正方形が重なっている部分の面積(図4の斜線部)について考えます。

(1)
次のときの重なっている部分の面積をそれぞれ答えなさい。
(ア)スタートしてから3秒後
(イ)スタートしてから4秒後
(ウ)スタートしてから5秒後
(2)
重なっている部分の面積が2cm2であるのは、スタートしてから何秒後ですか。
答え方の例にならって、すべて答えなさい。
例:1/2秒から2秒後の間と3秒後のとき
(答え方)1/2~2、3秒後
(3)
重なっている部分の面積が32/75cm2であるのは、スタートしてから何秒後ですか。
すべて答えなさい。
@解説@
(1)(ア)

3秒後は正方形の中心がBにくる。
1辺が1cm、辺の比が3:4:5の直角三角形をつくる。
この高さは、1×3/4=3/4cm
重なっている部分(青)は、1×1-1×3/4÷2=5/8cm2
(イ)
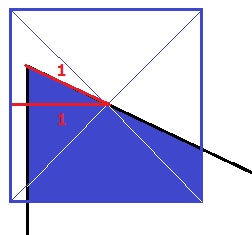
Bから斜辺を1cm進む。
正方形の左側の辺はBAの外側にある。
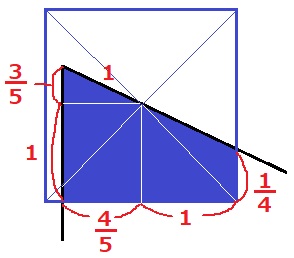
前図(ア)から右側の辺は、1-3/4=1/4cm
左上の直角三角形の高さは3/5cm、底辺が4/5cm。
重なり部分の台形は、(1/4+8/5)×9/5÷2=333/200cm2
(ウ)
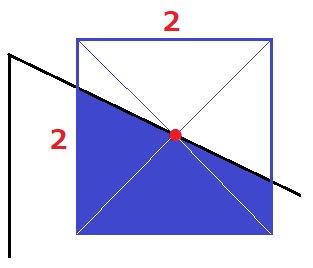
1直線が正方形の中心を通過する→正方形の半分。
2×2÷2=2cm2
(2)

(1)ウのように正方形の内部を1直線が切るような状態になると、半分の2cm2になる。
はじめは1cm移動して、正方形の下の辺がACに接するとき。
ここから正方形の右上の頂点がBCに接するときまで2cm2を保つ。
BO=1+3/4=7/4cm
移動距離OA;BA-BO=3-7/4=5/4cm
1~5/4秒後
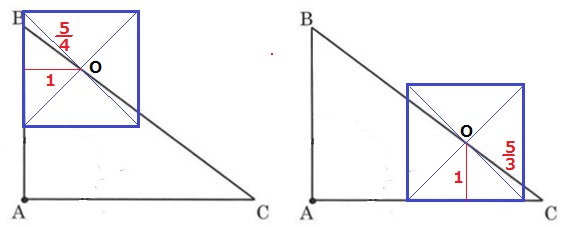
正方形の左の辺がBAに接してからスタート。
A~Oの距離;3+5/4=17/4cm
正方形の下の辺がACに接するまで続く。
OC=5/3cm、BO=5-5/3=10/3cm
移動距離A~O;3+10/3=19/3cm
17/4~19/3秒後
正方形の右上頂点がBCに接してからスタート。
移動距離;3+5+4/3+1=31/3cm
ゴールは正方形の左辺がABに接するとき。
移動距離;△ABCの外周-AO=(3+4+5)-1=11cm
31/3~11秒後
まとめると、1~5/4秒後、17/4~19/3秒後、31/3~11秒後。
(3)

正方形が頂点から離れると2cm2、頂点に近づくと重なり部分が小さくなる。
スタートのAが1cm2
Bは上図(1)アより5/8cm2
32/75cm2はこれより小さいのでC付近で起こるはず。
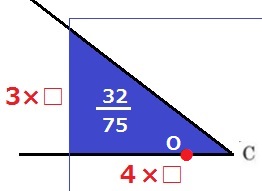
OがAC上にある場合を考える。
直角三角形の高さを3×□、底辺を4×□とする。
(3×□)×(4×□)÷2=32/75 ←両辺2倍
12×□×□=64/75 ←両辺÷12
□×□=64/(75×12)=16/225
□=4/15
(底辺)4×□=4/15×4=16/15cm
OC=16/15-1=1/15cm
Oの移動距離;3+5+1/15=121/15cm→121/15秒後
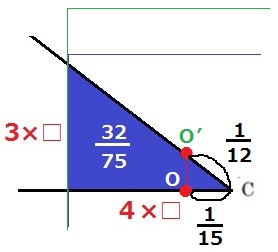
もう1つはBC上にある場合。
正方形の左側の辺が先ほどと重なる→中心はOの真上にある。
Oから真上に線をひき、BCとの交点をO’とする。
O’C:OC=5:4だから、
O’C=1/15×5/4=1/12cm
O’の移動距離;3+(5-1/12)=95/12cm→95/12秒後
95/12秒後と121/15秒後



コメント