問題ＰＤＦ
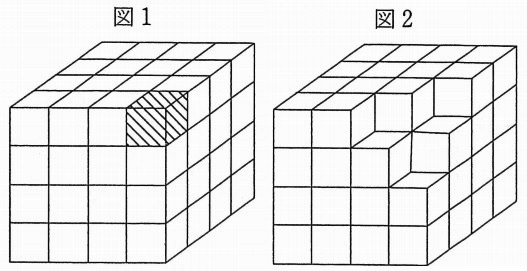
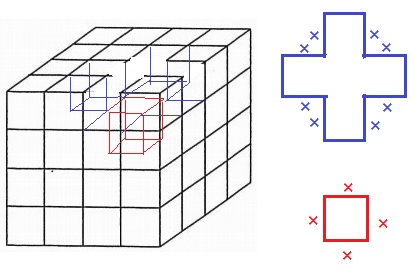
１辺の長さが１ｃｍの立方体を64個積み重ねて、１辺の長さが４ｃｍの立方体を作ります。色がぬられた立方体がある場合は、色がぬられた立方体と、それととなり合う立方体を取り除きます。例えば、図１のように色がぬられた立方体が１つあるときは、図２のように４つの立方体を取り除いた立体ができます。
①
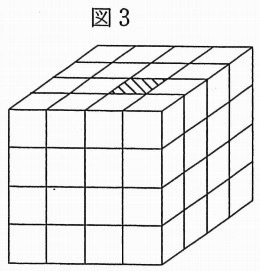
図３のように色がぬられた立方体が１つあるとき、できた立体の体積は何ｃｍ3ですか。
②
１番上の段に色がぬられた立方体が１つあるとき、できた立体の表面積は100ｃｍ2でした。
色がぬられた立方体の位置として考えられるものは何通りありますか。
③
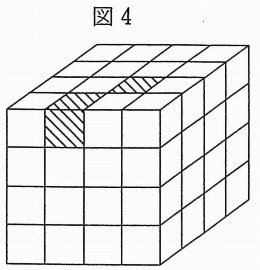
図４のように色がぬられた立方体が２つあるとき、できた立体の表面積は何ｃｍ2ですか。
＠解説＠
①
上から１段目が５つ、２段目が１つ取り除かれる。
64－６＝58ｃｍ3
②
取り除く前の表面積は、４×４×６＝96ｃｍ2
100ｃｍ2にするので＋４ｃｍ2になればいい。
１番上の段から１つ取り除く。
対称性から３パターンあり、赤か緑なら４通り、黒なら８通りが答えになる。
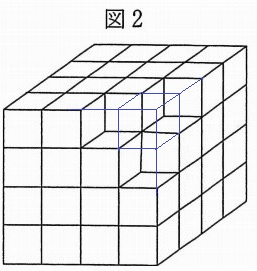
四隅の場合、図２をみると表面積は増減していない！
真ん中付近はどうか。
前問の様子を図示すると×の部分が増える。
取り除く部分は貫通しない（奥がある）ので減少分はなし。
＋12ｃｍ2だから違う。
四隅以外の端を試してみると、★の部分で＋４ｃｍ2
したがって、８通り。
③
実際の試験では１段目と２段目を上から見た図で攻略する。
★の部分が追加されるところ。
96＋10＝106ｃｍ2
難関中（算数科）解説ページに戻る
◆menu◆
公立高校入試…関東圏メイン。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント