2021年度　駒場東邦中学過去問【算数】大問４解説

問題ＰＤＦ
2021、6564のように、連続する２つの整数を並べてできた、
４けたの整数を考えます。

（１）
このような整数は、全部で何個ありますか。

（２）
このような整数すべての平均を求めなさい。

（３）
このような４けたの整数のうち、47の倍数をすべて求めなさい。

（２）
〔〇〇・〇〇〕

筆算を書いてみると、最後の☆☆は10～98と11～99の和。
10と99は１個、11～98が２個ずつある。

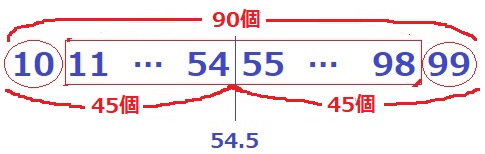
11～98は２個ずつだが、均すので１個ずつと捉えてもいい。
10～99の90個の整数で、（10―99）（11―98）…とペアで考えると、
45番目の54と46番目の55の平均である54.5が全体の平均になる。

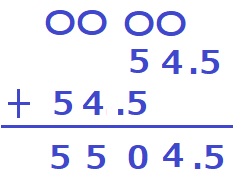
↑〇〇に54.5を挿入して強引に筆算。
5504.5

（３）
47の倍数とかいったいどうすれば( ;∀;)
47は素数なので倍数のルールは使えない。

43×47＝2021
これは年号問題で予想されていたので、１個は手堅くゲットできる。
大問題は2021の前に該当する47の倍数があるかということ。

◆前２桁＜後２桁
【1011、1112、1213、1314…1920】（10個）
1011÷47＝21…24
1112を47で割った余りを求める。
等差が101だから101÷47＝２…７
余りは７ずつ増えるので、1112÷47の余りは24＋７＝31
余りの数列⇒〔24、31、38、45…〕
これが47の倍数になれば余りが消えて47の倍数となる。
47－24＝23、23÷７は割り切れない！
47×２－24＝70、70÷７＝10で割り切れるが、
初項の余り24から余り７を10個足したものなので、初項の1011から11個目の数、
すなわち、2021だから、2021より前に47の倍数はないことになる。

◆前２桁＞後２桁
【1110、1211、1312、1413…1918】（９個）
1112を47で割ったときの余りが31だったので、
1110を47で割ったときの余りは29となる。
余りの数列⇒〔29、36、43、50…〕
47－29＝18、18÷７は割り切れない！
47×２－29は、47×２－24が割り切れたから割り切れません。
ということで、2021より前に47の倍数はない。
2021が連続する２数を並べた４桁の整数で最小の47の倍数である。

ここまでが長かった。。(;°;ω;°;)
しかし、このあとどうするか。。

４７４７
↑これはどう見えても47の倍数ですよね。
47の倍数に47の倍数を足したり引いたりしても47の倍数なので、
前２桁と後２桁が同数の4747から、差が１である2021をプラスマイナスして、
うまく調整できないものか。
4747－2021＝2726
4747＋2021＝6768

これで終わりと安心したいが、、4747×２＝9494でも同じことができる。
9494－2021＝7473
答えは、2021、2726、6768、7473。

＠別解＠
2021より前に47の倍数がない点ですが、
101の倍数±１で余りを一括して調べることもできます。
【1010、1111・1212・1313…1919】
1111÷47の余りが23で、余りは７ずつ増えるから、
余りの数列⇒〔23、30、37、44、51…〕
この数列にあらわれる数字を±１してそれが47の倍数になるかどうか。
19個しかないので、47と94に近いものだけを調べれば決着がつきます。
難関中（算数科）解説ページに戻る