問題ＰＤＦ
１辺１ｃｍの立方体を積み重ねて、図のような１辺10ｃｍの立方体をつくりました。
図の３つの円で囲まれた影の部分を、反対の面に垂直にまっすぐくりぬきます。
くりぬいても立方体はくずれないものとして、次の問いに答えなさい。
（１）
くりぬいた後の立方体の体積は何ｃｍ3ですか。
（２）
くりぬいた後の立方体の表面積は何ｃｍ2ですか。
（３）
さらに、図の長方形ＡＢＣＤの部分を、底面に垂直にまっすぐくりぬいたとき、
（２）と比べて表面積は何ｃｍ2だけ増えますか。
＠解説＠
（１）
全体…10×10×10＝1000ｃｍ3
くりぬくところ…
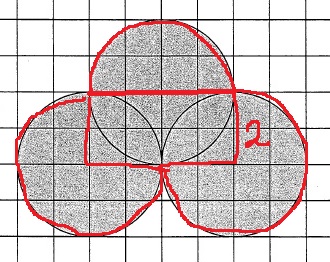
扇形は合わせると円２つ分に相当する。
（２×２×3.14×２＋２×４）×10
＝33.12×10＝331.2ｃｍ3
1000－331.2＝668.8ｃｍ3
（２）
くりぬく前の表面積は、10×10×６＝600ｃｍ2
くりぬいたことで、手前と奥の面は33.12ｃｍ2ずつ面積が減る。
空洞のなかには、円２つ分の円周×10ｃｍの面積が増える。
600－33.12×２＋２×２×3.14×２×10
＝600－66.24＋251.2＝784.96ｃｍ2
（３）
減るところから考える。
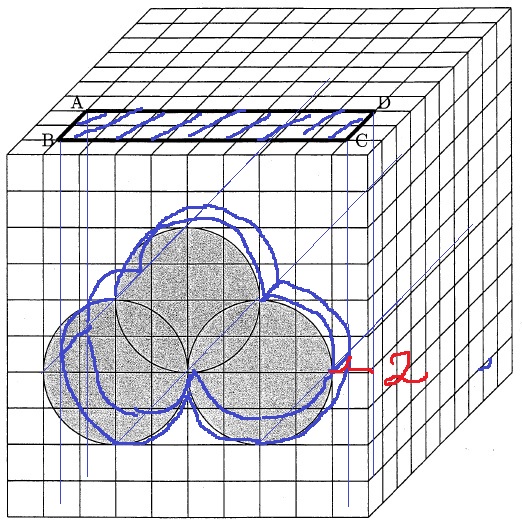
四角形ＡＢＣＤが上下の面で減る。２×８×２＝32ｃｍ2
また、１回目のくりぬきと接する部分が減り、
これは円２つ分の円周で、厚さ２ｃｍ分に相当する。
２×２×3.14×２×２＝50.24ｃｍ2
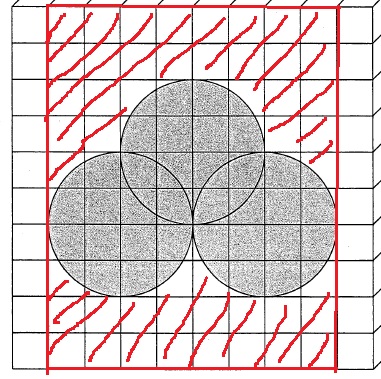
一方、増える場所は、赤い斜線の面積が空洞の前後にできる。
（８×10－33.12）×２＝93.76ｃｍ2
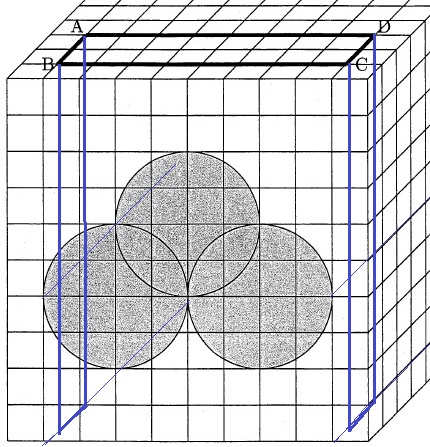
さらに、空洞の左右はフルに増える。
２×10×２＝40ｃｍ2
したがって、93.76＋40－32－50.24＝51.52ｃｍ2増える。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント