2020年度　専修大学松戸中学過去問【算数】大問７解説

問題ＰＤＦ
Ｓ中学校のＴ先生とＭさんが「11の倍数の見分け方」について会話しています。
あとの各問いに答えなさい。

Ｔ先生：Ｍさん、11の倍数の見分け方を知っていますか？
Ｍさん：３の倍数や４の倍数なら知っていますが、11の倍数は知りません。
Ｔ先生：それは、１けたおきに加えた和どうしの差を11で割るというものです。
たとえば、〔３８１７〕の場合、
１けたおきに加えた和➡３＋１＝４…(Ａ)、８＋７＝15…(Ｂ)
(Ａ)と(Ｂ)の差➡15－４＝11…(Ｃ)
(Ｃ)が11で割り切れるので、〔３８１７〕は11の倍数だとわかるのです。
もう一つ例をあげると、〔２５４８７〕の場合、
１けたおきに加えた和➡２＋４＋７＝13…(Ａ)、５＋８＝13…(Ｂ)
(Ａ)と(Ｂ)の差➡13－13＝０…(Ｃ)
この場合も(Ｃ)が11で割り切れるので、〔２５７８７〕は11の倍数だとわかります。
Ｍさん：へぇ～。びっくりしました。
Ｔ先生：それでは、さっそく問題です。
７けたの整数〔２Ｎ３０９５８〕が11の倍数になるとき、Ｎにあてはまる数は何ですか？
Ｍさん：はい。答えは〔　ア　〕です。
Ｔさん：正解です。よくできましたね。
Ｍさん：でも、Ｔ先生。どうしてそのようになるのですか？
Ｔ先生：それでは、99、9999、999999のように、９だけが偶数個並んだ数は
11の倍数になることを説明してみてください。
Ｍさん：はい。999999の場合で説明をすると、
999999＝990000＋9900＋99
＝11×90000＋11×900＋11×９
＝11×（90000＋900＋９）
＝11×〔　イ　〕
これでどうですか？
Ｔ先生：よくできました。
そうすると、９だけが偶数個並んだ数に11を加えた数も11になりますね。
ですから、
99＋11＝110、9999＋11＝10010、999999＋11＝1000010、…
も11の倍数です。ところで、これらの数の一の位の数字はすべて０ですから、
これらの数を10で割った数も11の倍数になりますね。
Ｍさん：つまり、11、1001、100001…のように、２個の１の間に偶数個の０が並ぶような数は
11の倍数だということですね。
Ｔ先生：その通り。
これらの性質を使うことで、11の倍数の見分け方がわかるのです。
たとえば、〔３８１７〕の場合で説明しましょう。
3817＝3000＋800＋10＋７
＝1000×３＋100×８＋10×１＋７
＝（1001－１）×３＋（99＋１）×８＋（11－１）×１＋７
＝1001×３－３＋99×８＋８＋11×１－１＋７
＝11×91×３－３＋11×９×８＋８＋11×１－１＋７
＝11×（91×３＋９×８＋１）－３＋８－１＋７
＝11×（91×３＋９×８＋１）＋（８＋７）－（３＋１）…(＊)
となります。　　の部分は11の倍数ですから、　　の部分が11の倍数であれば、
〔３８１７〕も11の倍数だとわかるのです。
Ｍさん：なるほど！よくわかりました。

（１）
次の①～④のうち、11の倍数はどれですか。すべて選びなさい。
①773124　②2701384　③9999999　④10000001

（２）
〔　ア　〕、〔　イ　〕にあてはまる数をそれぞれ答えなさい。

（３）
Ｍさんは家に帰ってから、Ｔ先生の説明にならって、
〔２５４８７〕が11の倍数になる理由を考えました。
下の式は、Ｔ先生が作った（＊）の式と同じ内容のものです。
〔　ウ　〕～〔　オ　〕にあてはまる数をそれぞれ答えなさい。
11×（〔　ウ　〕×２＋〔　エ　〕×５＋〔　オ　〕×４＋８）＋（２＋４＋７）－（５＋８）

（２）ア
奇数番目の位➡８＋９＋３＋２＝22
偶数番目の位➡５＋０＋Ｎ＝５＋Ｎ
両者の差が11の倍数か０になればいい。
22－（５＋Ｎ）＝17－Ｎ
０≦Ｎ≦９だから、Ｎ＝６

イ
中２で習う、整数の証明問題と考え方は同じです。
999999＝990000＋9900＋99
＝11×90000＋11×900＋11×９
＝11×（90000＋900＋９）
＝11×〔　イ　〕
イ＝90000＋900＋９＝90909
*11の倍数を証明したい場合、11×（整数）の形に変形する。

（３）
少々、問題文のおさらいを入れます(‘Д’)

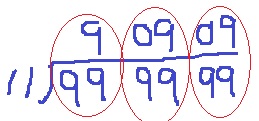
９が偶数個だと11の倍数になる証明は前問の通りだが、
筆算をかくと視覚的にわかりやすい。

（９が偶数個並ぶ数）が11の倍数なので、
（９が偶数個並ぶ数）＋11も11の倍数。
999999＋11＝1000010　←11の倍数
これは11の倍数×10の倍数なので、÷10した100001も11の倍数。

偶数番目の位である10、1000、100000…を（11－１）、（1001－１）、（100001－１）に、
奇数番目の位である100、10000、1000000を（99＋１）（9999＋１）、（999999＋１）に変換。
11、1001、100001、99、9999、999999はすべて11の倍数だから、
残りの数が11の倍数となれば全体で11の倍数となる。
残りの数とは〔１×各位の数〕の和で、偶数番目はマイナス、奇数番目はプラス。
偶数番目の位の和（マイナス分）と奇数番目の位の和（プラス分）の差が11の倍数か０になればいい。
例題の〔３８１７〕の場合、11×（91×３＋９×８＋１）＋（８＋７）－（３＋１）
　　　の部分は〔３８１７〕の８と７、３と１の和の差をしている。
これが、１桁おきに加えた和どうしの差を11で割れば11の倍数を判定できる理由。

25487
＝10000×２＋1000×５＋100×４＋10×８＋７
＝（9999＋１）×２＋（1001－１）×５＋（99＋１）×４＋（11－１）×８＋７
＝11×909×２＋２＋11×91×５－５＋11×９×４＋４＋11×８－８＋７
＝11×（909×２＋91×５＋９×４＋８）＋（２＋４＋７）－（５＋８）
　　　の部分が０なので、25487は11の倍数となる。
ウ…909、エ…91、オ…９
難関中（算数科）解説ページに戻る