問題ＰＤＦ
麗澤中学校で１年生の交流を深めるためにクラス対抗ラグビー大会を実施しました。
試合中の得点は、次のルールにしたがって点数が加算されます。
①トライ…５点、②コンバージョンゴール…２点、③ドロップゴール…３点
ただし、コンバージョンゴールはトライの回数以下です。
Ａ、Ｂ、Ｃ、Ｄの４クラスが参加し、総当たりのリーグ戦を行いました。
リーグ戦は次のルールにしたがって勝ち点を計算しました。
①勝ち…４点 ②引き分け…２点 ③負け…０点
④勝敗に関係なく、トライの回数が４回以上…１点
⑤負けた場合、点差が７点以内…１点
Ａ組とＢ組の対戦では、31－17でＡ組が勝利しました。
このとき、次の問いに答えなさい。
（１）
試合は全部で何試合行われたか答えなさい。
（２）
Ａ組とＢ組の対戦でのＡ組の点数の取り方は、何通りあるか答えなさい。
ただし、点数が加点された順番は考えなくてかまいません。
大会が進み、残りはＡ組とＤ組の対戦のみとなりました。
ここまでの結果として、次のことがわかっています。
・Ｃ組とＤ組の対戦では、Ｃ組が３回トライし17点差で勝利した。
・Ｂ組とＤ組の対戦は引き分けではなく、Ｄ組のトライの回数の方が多かった。
・Ｂ組とＣ組の対戦では、Ｃ組が３回トライしたがＢ組は負けなかった。
・Ａ組とＣ組の対戦では、Ａ組が２回トライし10点差で勝利した。
・Ｂ組の勝ち点は３、Ｄ組の勝ち点は４です。
なお、この大会の優勝クラスの決定方法は勝ち点が一番多かったクラスです。
ただし、勝ち点で並んだクラスがあったときは直接対決で勝ったクラスが優勝とします。
（３）
Ａ組とＤ組の対戦が終了し、Ｄ組が優勝したとき、
各組の勝ち点の組み合わせは何通りあるか答えなさい。
＠解説＠
（１）
４組で総当たり戦（リーグ戦）
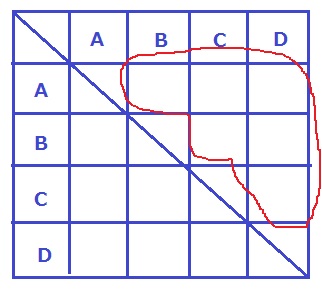
↑こんなヤツです。６試合
（２）
31点の中身を調べる。
＠条件＠
トライ…５点、コンバージョンゴール…２点、ドロップゴール…３点
ただし、コンバージョンゴールはトライ以下の回数。
得点の大きいトライの回数で場合分け。
■トライ６回
31－５×６＝１点
残り１点が作れないので×。
■トライ５回
31－５×５＝６点
２×３と、３×２の２通り。
■トライ４回
31－５×４＝11点
２×４＋３と、２＋３×３の２通り。
■トライ３回
31－５×３＝16点
２×２＋３×４の１通り。
■トライ２回
31－５×２＝21点
３×７の１通り。
■トライ１回
31－５×１＝26点
２×１＋３×８の１通り。
■トライ０回
残り31点を作れない×。
したがって、７通り。
*トライが多いときはドロップ、少ないときはコンバージョンで場合分けした方が良いかな？
（３）
推論問題。条件がフクザツで厳しい(´Д｀)
この問題に精を尽くすより、他を確実にとった方が良いです。
だいたいこの手の問題は、最後に挙げられた情報が一番重要であったりする。
Ｂの勝ち点は３、Ｄの勝ち点はＤ
〔ＢvsＣ〕でＢが勝ってしまうと、Ｂの勝ち点が＋４になってしまう。
ＢとＣは引き分けとなる。Ｂはトライ４回以上の可能性あり。
同様に、〔ＢvsＤ〕でＢが勝つとＢの勝ち点が＋４になってしまう。
Ｂは負け、Ｄが勝ち。いずれもトライ４回以上の可能性はあり、
Ｂはドロップゴールをたくさん決めて７点差以内で負けたかもしれない。
だが、ＤはＢとの勝利で勝ち点が４なので、これまでに追加点はなかったことになる。
これを踏まえたうえで条件を整理する。
トライの回数が４回以上、もしくは負けても７点差以内でもらえる１点の処理がキツイ。
この１点が不明な場合、以下、△とあらわす。
〔ＡvsＢ〕Ａ：４＋△ Ｂ：０
*勝ったＡは４点、負けたＢは０点。
前問のようにＡは31点のうち、トライが４回以上の場合がある。
Ｂは14点差で負け、17点ではトライは最大で３回だから追加点はない。
〔ＡvsＣ〕Ａ：４ Ｃ：０＋△
*Ａはトライ２回で追加点なし。Ｃはトライ４回以上がありうる。
（たとえば、Ｃがトライだけで５×４＝20点。Ａは５×２＋２×１＋３×６＝30点のとき）
〔ＡvsＤ〕まだ行われていない。
〔ＢvsＣ〕Ｂ：２＋△ Ｃ：２
*Ｂはトライ４回以上の可能性あり。
〔ＢvsＤ〕Ｂ：０＋△＋△ Ｄ：４
*Ｂはトライ４回以上、もしくは７点差で負けた可能性あり。
〔ＣvsＤ〕Ｃ：４ Ｄ：０＋△
*Ｃはトライ３回で追加点なし。Ｄはトライ４回以上の可能性がある。
（たとえば、Ｄはトライだけで５×４＝20点。Ｃは５×３＋２×２＋３×６＝37点のとき）
現時点で勝ち点は少なくともＡ８点、Ｂ２点、Ｃ６点、Ｄ４点。
Ｂの勝ち点は３なので、どこかの△が１だが、
ＡとＤの対戦でこれ以上は増えない。Ｂは勝ち点３で確定。
最終的にＤが優勝するので、ＤはＡに勝つことになる。
〔ＡvsＤ〕Ａ：０＋△＋△ Ｄ：４＋△
Ａ８点、Ｂ３点（確定）、Ｃ６点、Ｄ８点。
■ＡとＤの勝ち点が同点
この場合、直接対決で制したＤが優勝するので条件に適合する。
Ａの△は３つ、Ｄの△は１つ。
（Ａ、Ｄ）＝（８、８）（９、９）の２通り。
■Ｄの勝ち点がＡより大きい
（Ａ、Ｄ）＝（８、９）の１通り。
さらに、Ｃに△が１つあるので、Ｃの勝ち点は６か７で２通りある。
よって、各組の勝ち点の組み合わせは、（２＋１）×２＝６通り
*実際の試合でドロップゴールは難しい。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント