問題PDF
Aさん、Bさん、Cさん、Xさんの所持金はそれぞれ1600円、3000円、4000円、x円です。
AさんとXさんの所持金の差はa円、BさんとXさんの所持金の差はb円、
CさんとXさんの所持金の差はc円です。a、b、cはすべて異なる数です。
次の問いに答えなさい。(1)と(2)は下のなかから選んで答えなさい。
①a<b<c ②a<c<b ③b<a<c
④b<c<a ⑤c<a<b ⑥c<b<a
(注意)例えば①は、bがaよりも大きく、cよりも小さいことを表しています。
(1)
a、b、cの大小関係についてありえないものを、①~⑥からすべて選びなさい。
(2)
bとcの和がaの2倍に等しいとき、a、b、cの大小関係として考えられるものを、
①~⑥からすべて選びなさい。
(3)
bとcの和がaの2倍に等しいとき、Xさんの所持金x円はいくらですか。
@解説@
(1)
最小Aと最大Cだけで考える。
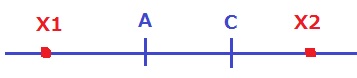
数直線でXを左右に移動させる。
X<Aのとき、Aの方がXに近いのでa<c
X>Cのとき、Cの方がXに近いのでc<a
ということは、aとcの大小関係は決まらない。
あいだのBに狙いを絞る。
XがBに近ければ、bが最小になる。
反対に、bが最大となる場合はあるのか?
XがA以下だと最大はc、XがC以上だと最大はa。
では、XがAとCのあいだのときはどうか。
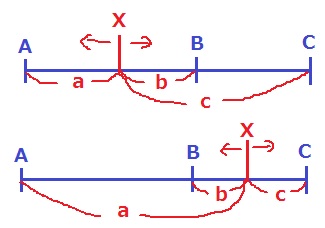
bが最大になる(BがXから最も離れる)ことはない。
よって、bが最も大きい②と⑤がありえない。
(2)
b+c=a×2
平均を思い浮かべる。
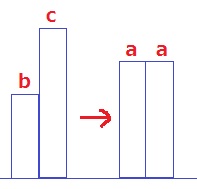
bとcの間にaがあり、bは最大ではないので、b<a<cとなる。
すべて式だが、答えは③だけ。
(3)
実際の試験では求め方の過程も記述する。
中学数学の先走りのような・・。
b<a<c
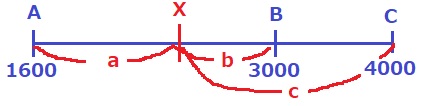
c=b+1000
b+c=a×2のcにb+1000を代入(cをb+1000に入れ替える)
b+(b+1000)=a×2
b×2+1000=a×2 ←すべてを÷2
b+500=a(aとbの差が500)
AとBの差は3000-1600=1400
a+b=1400(aとbの和が1400)
aとbの和と差がわかったので和差算。
b=(1400-500)÷2=450
X=3000-450=2550



コメント