2023年度　早稲田中学２回目過去問【算数】大問５解説

問題ＰＤＦ
ある国には、貨幣として４円玉、９円玉、12円玉、25円玉の４種類の硬貨しかありません。
次の問いに答えなさい。

（１）
ちょうど支払うことのできない金額は全部で何通りありますか。

（２）
2023円の商品を買うとき、ちょうど支払うために必要な硬貨は最も少なくて何枚ですか。

（３）
Ａさんがもっている硬貨の枚数は、Ｂさんがもっている硬貨の枚数より１枚少ないですが、
その金額は同じでした。このような金額のうち、最も少ないのは何円ですか。

（４）
ＰさんとＱさんはそれぞれ組み合わせが違う４枚の硬貨をもっていて、
その金額は同じでした。このような金額のうち、最も少ないのは何円ですか。

＠解説＠
（１）
金額を小刻みに調節しやすいのは安い硬貨である。
そこで、４円と９円を使って支払えない金額を求めてみる。

１行４つの数列を書く。
右の列は４の倍数だから、４だけで作れるので除外。

（２）
すべて25円硬貨で支払ったとすると、2023÷25＝80枚…23円
前問より、23円は４枚の硬貨で支払えない金額であった。
そこで、25枚硬貨を79枚とすると、残りの金額は23＋25＝48円
48円＝12円×４枚
79＋４＝83枚

もし、25円硬貨を78枚とすると、残りは48＋25＝73円
73円を25円硬貨以外で払おうとすると、６枚以上は必要である。
よって、最も少ない枚数は83枚。

（３）
３種類以上の硬貨を使うパターンもあるので迷う..。
（１）より答えは24円以上である。

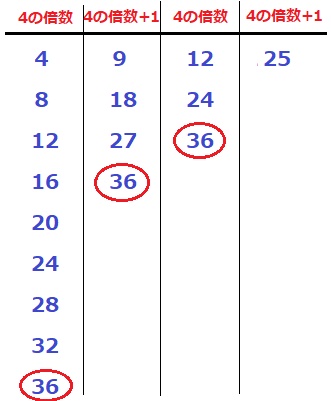
４と12は４の倍数、９と25は４の倍数＋１。
４×３＝12→４円硬貨と12円硬貨は２枚差で同額になる→１枚差で同額は作れない。
４の倍数＋１である９円硬貨と25円硬貨同士でも無理。

そこで、４の倍数と４の倍数＋１の組み合わせを考える。
25円硬貨を１枚使うとき、25＝４＋９＋12（１枚と３枚）→２枚差で不適。
25円を２枚使うと金額が大きくなるので、９円硬貨に絞って考えてみる。

９円硬貨を４枚集めると４の倍数になる。
９×４＝４×９＝12×３
９円硬貨４枚と12円硬貨３枚で１枚差の同額となる。
よって、36円。

＠余談＠
25円硬貨を１枚使うと不可能。
残りの４・９・12の最小公倍数36から、これに当たりをつけてしまうのも手かな…。

（４）
４枚の硬貨の種類が異なりつつ、金額が同じになった。

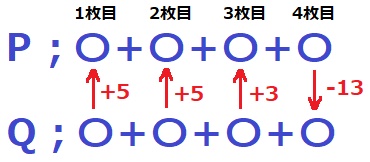
たとえば、１枚目はＰの方が５大きい、２枚目も５大きい、３枚目は３大きく、
４枚目はＱの方が13大きい場合、＋13と－13で差の合計がプラスマイナスゼロになる。
つまり、差の合計がゼロになると４枚の硬貨の合計は等しくなる。

そこで、各硬貨の差をとってみる。

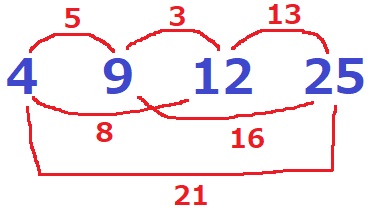
金額を少なくするので、４円と９円の組み合わせをできるだけ増やす。
差【５＋５＋３＝13】
Ｐ；４＋４＋９＋25
Ｑ：９＋９＋12＋12＝42円

・・と思ったのですが、コメ欄にてご指摘がございました。
１枚は互いに４円硬貨を持って差を０にするパターンがありました。
差【０＋５＋８＝13】
Ｐ；４＋４＋４＋25
Ｑ；４＋９＋12＋12＝37円
答えは37円。コメント感謝です。
難関中（算数科）解説ページに戻る