2019年度　早稲田中学過去問２回目【算数】大問４解説

問題ＰＤＦ
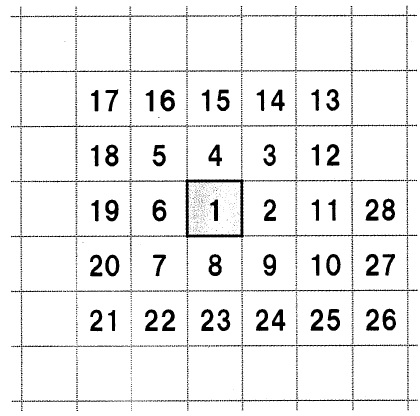
整数を１から順に下の図のようなます目に並べていきます。
図は28までを並べたところです。
ます目にある数の位置を、１の書いてあるますを基準にして、
（左か右に進んだ数、上か下に進んだ数）
と表すことにします。
例えば、３の位置は（右１、上１）、20の位置は（左２、下１）、23は（０、下２）
28の位置は（右３、０）と表されます。次の問いに答えなさい。

（１）
（右５、上５）にある数は何ですか。

（２）
144の位置を答えなさい。

（３）
（右11、下９）にある数は何ですか。

（４）
2019の位置を答えなさい。

（１）
マス目があるので、機械的に手を動かして書いてみる。

（右４、上４）は57だが１歩足りず。
斜め右の数列は【１・３・13・31・57・・】
増加数は（２・10・18・26・・）
増加数の増加数は８で一定。
次の増加は、26＋８＝34なので、
（右５、上５）は、57＋34＝91

＠余談＠
１から右に行っても増加の増加は８。
【１・２・11・28・53・・】
53の次は86。86に５を足して91。

１から上にいっても同様。
【１・４・15・34・61・・】
61の次は96。96から５を引いて91。

（２）
144は12の平方数。

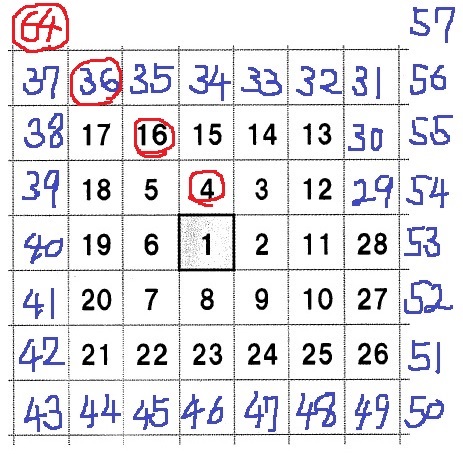
（０、上１）⇒４
（左１、上２）⇒16
（左２、上３）⇒36
２の平方数が上１、４の平方数が上２、６の平方数が上３なので、
12の平方数は上６となる。
左に進む数は、上に進む数－１。
よって、144は（左５、上６）

＠余談＠
４の反対側【２・10・26・50…】は２つの偶数の平方数の平均。
10＝４と16の平均。26＝16と36の平均。50＝36と64の平均。
ちょうど半周する位置にある。

（３）
奇数の平方数は見つけやすい。

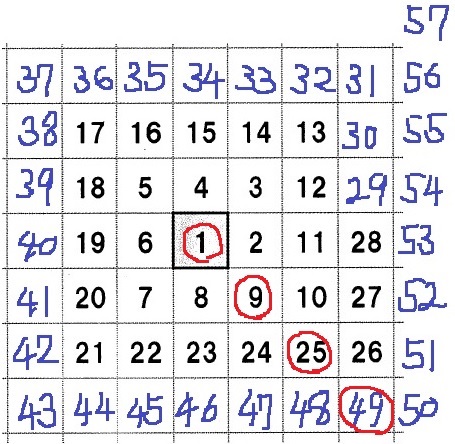
（右１、下１）⇒３の平方数９
（右２、下２）⇒５の平方数25
（右３、下３）⇒７の平方数49
（○の平方数－１）÷２＝進んだ数
（右９、下９）→９×２＋１＝19⇒19の平方数361

お隣の（右10、下９）は362。
しかし、右11はグルっと１周したあとなので途方に暮れる…。

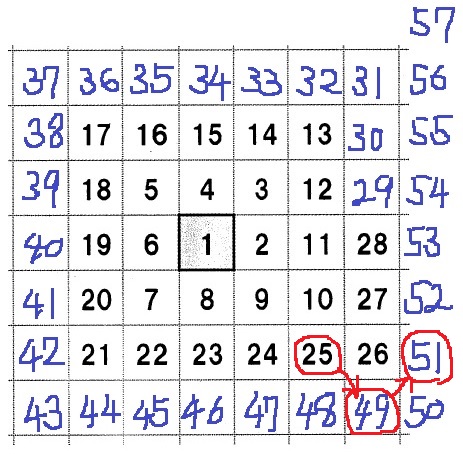
25の２つ右隣りは49から２を足す。
右下を経由して右上に行く。

（右10、下10）は21×21＝441
（右11、下９）は441＋２＝443

（４）
奇数の平方数が最も計算しやすいので、ここから攻め入る。
30×30＝900
40×40＝1600
50×50＝2500

2019に近い奇数の平方数は、40～50の範囲にある。
45×45＝2025
（45－１）÷２＝22
2025は（右22、下22）
2019は同じ行で左に６なので、（右16、下22）
難関中（算数科）解説ページに戻る