問題ＰＤＦ
図のような的に矢を３回射って、そのうち高い２回の点数の平均を最終得点とするゲームがあります。
Ｊ子、Ｇ子、Ｋ子がこのゲームをしたところ、次のようになりました。
Ｊ子の最終得点は〔 〕点、Ｋ子の３回の点数は低い方から順に、
１点、〔 〕点、〔 〕点でした。
＠解説＠
こういう問題は大抵、うしろに書かれてある条件が突破口になる。
『３人の最終得点の平均は４点』→３人の最終得点の合計は12点。
『最終得点はＪがＧより１点高い』
ここで、３人の最終得点の組み合わせを考える。
最終得点は得点の高い２回の点数の平均なので、整数もしくは小数第一位が５（.5）のどちらか。
（Ｊ、Ｇ）＝（５、４）とすると、Ｋの最終得点は12－（５＋４）＝３点
ＪとＧの点差に配慮して調べていくと、
（Ｊ、Ｇ、Ｋ）＝（５、４、３）（4.5、3.5、４）（４、３、５）
*Ｊ＝3.5、Ｇ＝2.5にすると、Ｋ＝６となって不適。
また、最終得点が５点だと最高得点の５点を２回出さなくてはならないが、
『２回以上同じ点数を取った人はいない』ので不適。
（Ｊ、Ｇ、Ｋ）＝（4.5、3.5、４）が確定する。
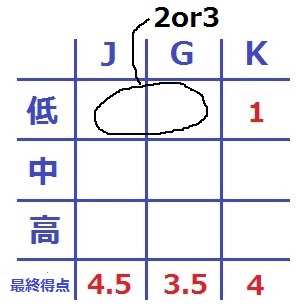
１回目、２回目…ではなく、得点の低い順に低・中、高として表でまとめる。
低が４だと、中・高が５でかぶるので×。
Ｋの低が１点だから、ＪとＧの低は２点か３点。
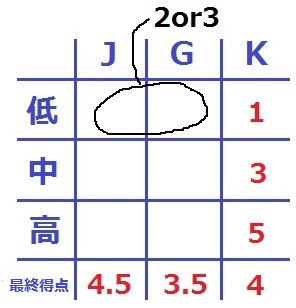
求めたいのはＫの得点だが、得点は整数値で中と高の平均が４点…
→３点と５点しかない！
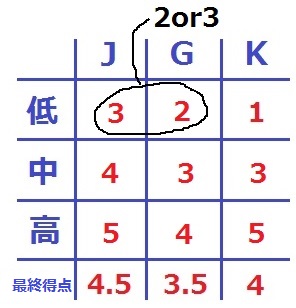
Ｊの最終得点…4.5点、Ｋの得点…３点と５点
＠余談＠
全部埋めるとこうなります。
難関中（算数科）解説ページに戻る
コメント