2019年度　明治大学付属中野中学過去問【算数】大問３解説

問題ＰＤＦ
（１）
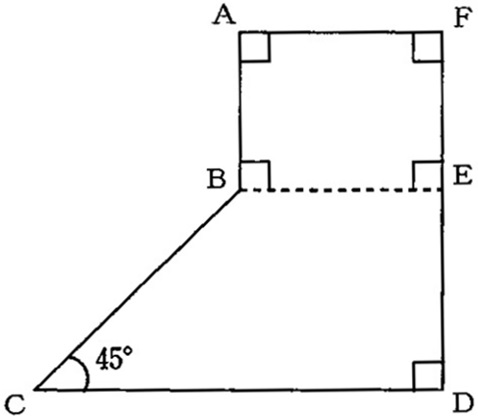
下の図は長方形と台形を組み合わせた図形で、面積は48ｃｍ²です。
長方形ＡＢＥＦと台形ＢＣＤＥの面積比が１：３で、ＤＥ＝４ｃｍのとき、
点Ａと点Ｃを結んでできる三角形ＡＢＣの面積を求めなさい。

（２）
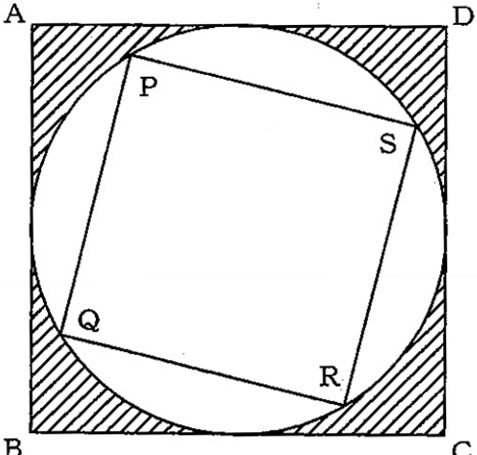
下の図のように、正方形ＡＢＣＤの中に、この正方形の一辺の長さを直径とする円が入っています。さらにその円の中に、円周上に頂点を持つ正方形ＰＱＲＳがあります。正方形ＰＱＲＳの面積が12ｃｍ²のとき、斜線部分の面積を求めなさい。

＠解説＠
（１）
長方形：台形の面積比が１：３なので、それぞれの面積は12ｃｍ²と36ｃｍ²。

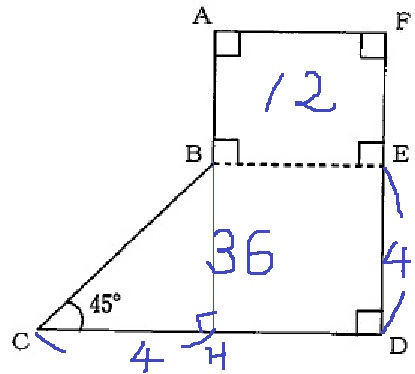
Ｂから垂線をおろし、交点をＨとする。
△ＢＨＣは内角が45°ー45°―90°の直角二等辺三角形。

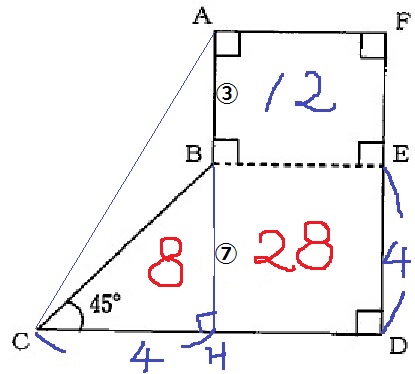
△ＢＨＣ＝４×４÷２＝８ｃｍ²
四角形ＢＨＤＥ＝36－８＝28ｃｍ²ＡＢ：ＢＨ＝四角形ＡＢＥＦ：四角形ＢＨＤＥ＝12：28＝③：⑦
△ＡＢＣ：△ＢＨＣの面積比も３：７なので、
△ＡＢＣ＝８×③/⑦＝24/７ｃｍ²

（２）
内部の正方形ＰＱＲＳを回転させる。

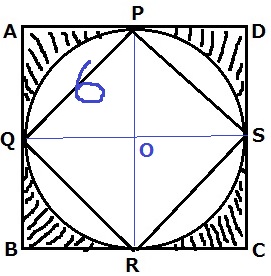
正方形ＰＱＲＳの面積の２倍が、正方形ＡＢＣＤとなる。
正方形ＡＢＣＤ＝24ｃｍ²
正方形ＡＱＯＰ＝24÷４＝６ｃｍ²
円の半径×半径は６なので、
斜線部分の面積は、24－６×3.14＝5.16ｃｍ²
難関中（算数科）解説ページに戻る

◆menu◆ 公立高校入試…関東圏メイン。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→