問題PDF
ある製品を、Aさんが休まずに1人で作ると45分かかり、
Bさんが休まずに1人で作ると30分かかります。
この製品を2人で作りはじめ、それぞれ途中で休みをとり、
23分後に製品を完成させました。
このとき、次の各問いに答えなさい。
(1)
2人が同じ時間だけ休んだとすると、Aさんは何分間休みましたか。
(2)
BさんがAさんより5分多く休んだとすると、Bさんは何分間休みましたか。
@解説@
(1)
典型的な仕事算。
1分あたり、Aは1/45、Bは1/30完成させる。
2人が休まずに作業をすると、1分あたりの作業量は1/45+1/30=1/18
→18分で完成することになる。
『2人が同じ時間を休む』ので、23-18=5分間
(はじめに2人が休まずに働いて18分で完成し、
その後2人で5分休憩して23分で完成したと考えればいい)
(2)
BがAより5分多く休み、23分で完成させる。
先ほどは2人が5分ずつ休んで23分だったので、
同じ時間で完成したということは、『休んだ量』が(1)と等しい。
(仕事算…ではなく休憩算)
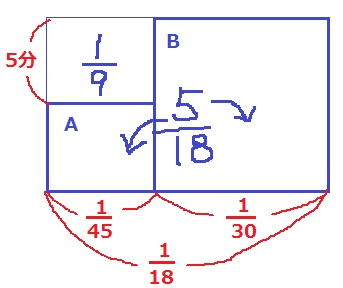
横の長さは1分あたりに休んだことでサボった仕事の量(休んだ量)
縦の長さが休憩時間。面積が休んだ量。
AとBの面積の合計は2人で5分間休んだ量、すなわち5/18。
左上の長方形が、1/45×5分=1/9
全体の面積は、1/9+5/18=7/18
Bの縦の長さ(Bが休んだ時間)は、7/18÷1/18=7分間
@@@
算数大好きさん(@kimagure_mana)より素敵な解法を頂きました。
(1)全体の仕事=[90]
Aの仕事量=[2]/分 Bの仕事量=[3]/分
A,B2人ですると,[90]÷([2]+[3])=18分
(2)Aが□分休んだとすると,
<休んだ仕事>=<フォローした仕事>より,
[5]×□+[3]×5分=[5]×(23-18)分 が成立するので,
□=([5]×5-[3]×5)÷[5]=2分
Bが休んだのは,5+2=7分…(答)
全体の仕事量を30と45の最小公倍数90とすることで、
その後の計算を整数で抑えております。
そして、休んで穴が開いた仕事量とそれをフォローする仕事量で等式を立てます。
この等号関係は押さえておきたいポイントですね。



コメント