2023年度　雙葉中学過去問【算数】大問４解説

問題ＰＤＦ
大きさの異なる円柱の水そうＡ、Ｂ、Ｃがあります。
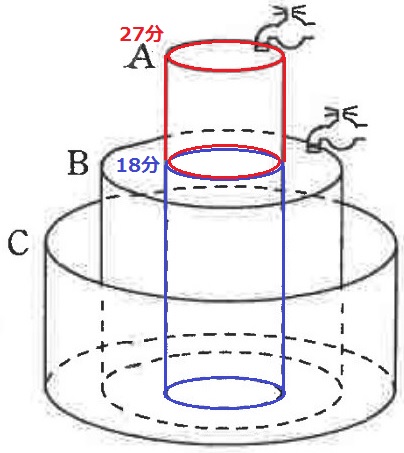
Ａ、Ｂ、Ｃを図のように組み合わせ、底面を固定しました。

上の蛇口からＡに、下の蛇口からＢに、毎分同じ量の水を、一定の割合で同時に入れ始めました。
水を入れ始めてから、
・14分後に、Ｂから水があふれ始めました。
・18分後に、ＡとＢの水の高さが同じになりました。
・27分後に、Ａから水があふれ始めました。
ただし、水そうの厚さは考えません。

（１）
ＡとＢの水そうの高さの比を求めましょう。

（２）
ＡとＢの底面の半径の比を求めましょう。

（３）
ＢとＣの水そうの高さの比は、ＡとＢの水そうの高さの比と同じです。
Ｃの底面の半径はＡの底面の半径の２倍です。
Ｃから水があふれ始めるのは、水を入れ始めてから何分何秒後ですか。

（１）

Ａだけを見る。
18分後にＢと同じ高さ（青）、27分後に上の部分（赤）が満たされてあふれる。
高さの比は、Ａ：Ｂ＝27：18＝３：２

（２）

Ｂだけを見る。
14分後に赤い部分、18分後に青い部分が満たされる。
赤：青＝14：18＝⑦：⑨
底面積の比は、Ａ：Ｂ＝⑨：（⑦＋⑨）＝⑨：⑯
底面積の比は半径×半径の比なので、半径の比はＡ：Ｂ＝３：４

（３）

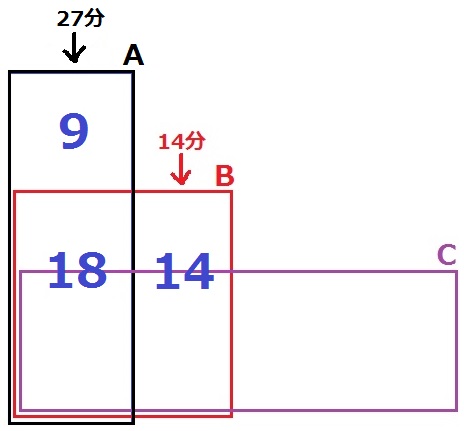
３つの水槽を端に寄せ、横からみた面積で考える。
蛇口１本が１分間に水を入れる部分の体積を１とする。
水槽Ａにおいて水槽Ｂの高さまでの体積が18、それより上が９。
水槽Ａを除いた水槽Ｂの体積が14。

（１）の解答と問題文より、水槽Ｂと水槽Ｃの高さの比は③：②。
水槽Ａの18を①：②に分けると、上の体積は６、下は12。
水槽Ｂの上は14/３。

半径の比はＡ：Ｃ＝１：２
底面積の比はＡ：Ｃ＝①：④
水槽Ｃの体積は、12×④＝48
全体の体積は、48＋６＋９＋14/３＝203/３
これを蛇口２本で満タンにするから、
203/３÷２＝203/６＝33・５/６分＝33分50秒後
難関中（算数科）解説ページに戻る