問題PDF
(1)
図1の四角形ABCDにおいて、角(あ)の大きさは何度ですか。
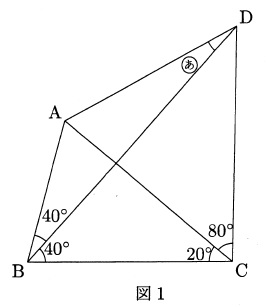
(2)
図2の三角形ABCにおいて、点Dは辺AB上に、点Eは辺AC上にあります。
辺BCの長さとBFの長さが同じになるように、辺AC上に点Fをとります。
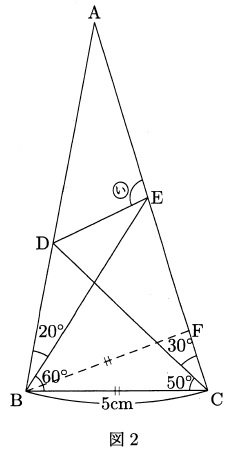
①次のア~エの中から、長さが5cmであるものをすべて選びなさい。
ア:BD イ:BE ウ:CD エ:EF
②角(い)の大きさは何度ですか。
@解説@
(1)

・・パッと見、なんか怪しい。
40°で等角のはずなのに、下の40°の方が大きく見える。
80°と20°も4:1なのに、開き具合が4:3くらいになっている。
図がいい加減なのでは?
とりあえず、わかる角度を調べていく。
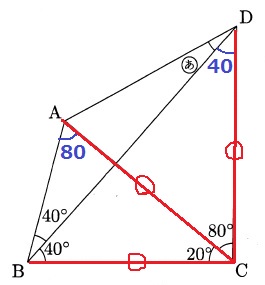
△ABCと△BCDの内角から、この2つの三角形は二等辺。
ここから、△ACDも二等辺だとわかる。
よって、(あ)=(180-80)÷2-40=10°
@@
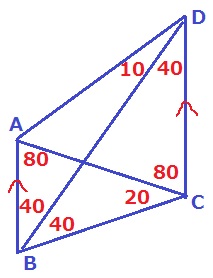
↑正しい図を描くとこうなる。
∠ABD=∠BDC=40°、∠BAC=∠ACD=80°から、
錯角が等しいので、ABとDCは平行である。
(2)①
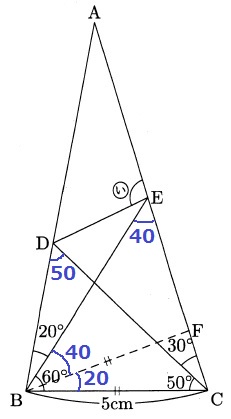
△BCDで、∠BDC=180-60-50=50°
△BCDはBC=BDの二等辺。(BD〇、CD×)
△BCEで、∠BEC=180-60-80=40°
△BCEは角度がバラバラな不等辺三角形。(BE×)
∠EBF=60-20=40°
△BEFは二等辺。BF=EF(EF〇)
よって、ア・エ。
②
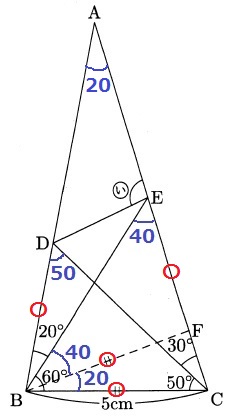
できそうでできない(´゚ω゚`;)
△ABCが二等辺である点に注目しても無理。
本問は数学界で有名な図形なのだが、小6にこの知識を要求するのは酷なので、
わざわざ与えられたBFに着目する。
①でこれと等しい辺を確認したので、BFと〇の辺をよく観察してみると、
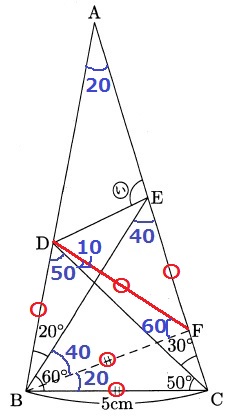
DFに補助線ひくと正三角形BDFを発見!
(BD=BFで、あいだの角DBFが60°だから)
∠CDF=60-50=10°

△DCFで外角定理→∠DFE=10+30=40°
△DEFは二等辺→∠FDE=(180-40)÷2=70°
△DEFで外角定理→(い)=70+40=110°
@@
元ネタが気になった人は『ラングレー 問題』で検索してみましょう。
ラングレーは他にもさまざまなパターンがあるようです。

Ikuro’s Home Pageより。
正十八角形の対角線の交点と同じらしい…こんなの発見するとは相当の暇人だな(´゚д゚`)



コメント