問題PDF
あるスポーツの複合競技を5人の選手で競います。まず、3つの基本種目A、B、Cを順に行います。それぞれの基本種目では、2人以上が同じ順位になることはありません。次に、基本種目A、B、Cの順位の数字をすべてかけ合わせた数を得点にします。さらに、得点の低い選手が上位となるように、総合順位を決めます。
例えば、基本種目Aで3位、Bで2位、Cで3位となった選手の得点は18点です。また、得点が18点の選手は、20点の選手よりも総合順位は上位となります。
(1)
得点としてありえない整数のうち、最も小さいものはいくつですか。
ただし、0は考えないものとします。
(2)
基本種目AもBも1位であった選手がいましたが、総合順位が1位となったのは別の選手でした。
総合順位が1位となった選手の得点は何点ですか。
(3)
5人の選手の得点に同じものはなく、また、総合順位が4位、5位の選手の得点は、
それぞれ16点、80点でした。総合順位が1位、2位、3位となった選手の得点はそれぞれ何点ですか。
(4)
基本種目AとBの順位の数字をかけ合わせた数は、3人だけが同じでした。
総合順位が1位となった選手の得点が12点であるとき、選手全員の得点の平均は何点ですか。
@解説@
スポーツクライミングの得点方式です。
(1)
□×□×□の積でありえない数のうち、最小数を求める。
各基本種目では同順位はいないので1~5位がすべている。
⇒□は1~5の範囲。
1×1×(1~5)=1~5
1×2×3=6
7は素数で無理。よって、7。
(2)
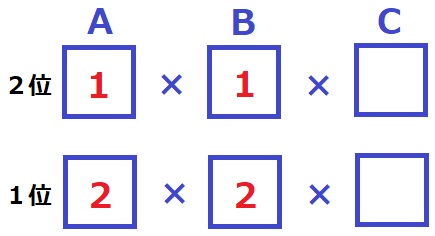
AとBで1位だった者が総合で2位になったとする。
総合1位の得点は積を小さくするので、AとBの順位を2位にしておく。

Cの得点はこの組み合わせしかない。
総合1位の得点は4点。
(3)
総合5位の80点は【4】×【4】×【5】しかない。
総合4位の16点は【1】×【4】×【4】か【2】×【2】×【4】だが、
前者だと2種目が4位となり、総合5位も2種目で4位だから、
4位が同種目で重複することになる。よって、総合4位は【2】×【2】×【4】
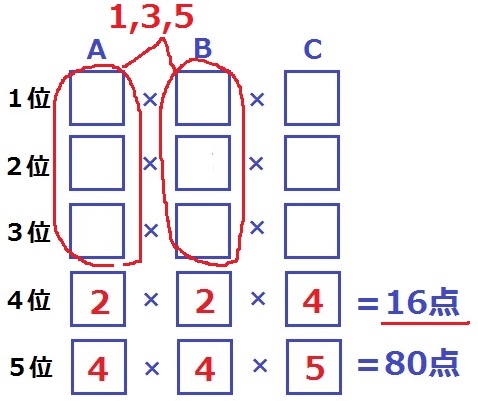
AとBには残り1・3・5が入る。
4位が16点であることに注目!
5を含む16未満は【5】×【1】×【1】、【5】×【2】×【1】、【5】×【3】×【1】
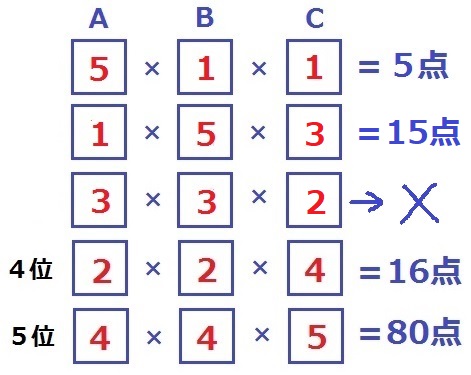
【5】×【1】×【1】を採用すると、うまくいかない…。
【1】を分けて、【5】×【2】×【1】と【5】×【3】×【1】にすると、
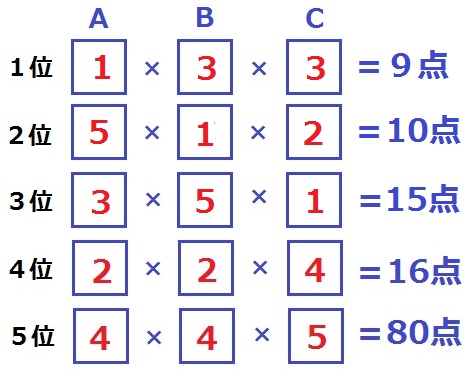
うまくいく。
1位…9点、2位…10点、3位…15点
(4)
□×□の積が3人だけ同じになった。
□に3や5をいれた場合、【1】×【3】、【3】×【1】といったように、
順番をひっくり返して2個は作れるが3個目が作れない。
【1】×【4】=【4】×【1】=【2】×【2】しかない。
A×Bの積は『3人だけが同じ』⇒残りの2人は【3】×【3】、【5】×【5】
1位の選手の12点は、【1】×【3】×【4】か【2】×【2】×【3】のどちらか。
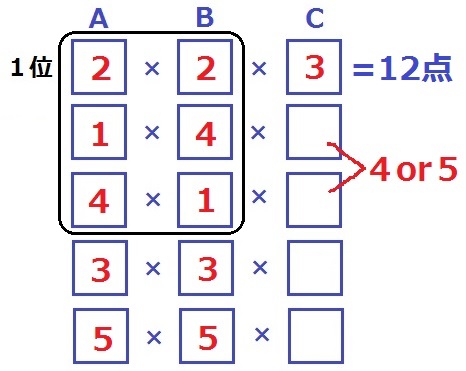
もし、1位が【2】×【2】×【3】の場合。
A×B=12である残り2人のCは、12点を超すように【4】か【5】でなくてはならないが、
4位が重複してしまうので不適!×
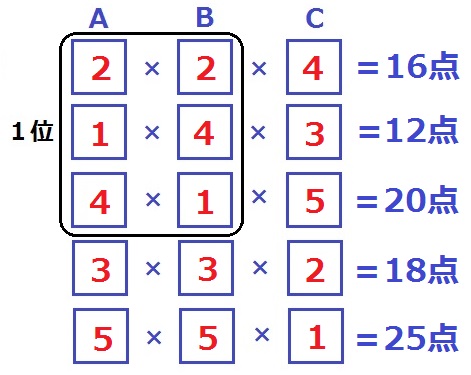
1位が【1】×【4】×【3】だと、うまい具合にいける。
5人の平均点は、(16+12+20+18+25)÷5=18.2点




コメント