問題PDF
次の各問いに答えなさい。
ただし、角すいの体積は、(底面積)×(高さ)÷3で求められるものとします。
(1)
【図1】のように、立方体の展開図に点線をひきます。もとの折り目に加え、点線部分も折り目とし、すべての折り目が立体の辺になるようにして、この展開図を組み立てると、【図2】のような立体ができました。この立体の体積は何cm3ですか。

(2)
【図3】のように、正方形BECDの対角線を一辺とする正三角形ABCを考えます。【図4】の展開図において、(あ)~(え)は合同な二等辺三角形で、(お)~(く)は【図3】の正三角形ABCと合同です。この展開図に組み立てて立体を作ると、二種類の立体が作れます。そのうち、体積が大きい方の立体を立体A、立体が小さい方の立体を立体Bとします。立体Aの体積は、立体Bの体積より何cm3大きいですか。

(3)
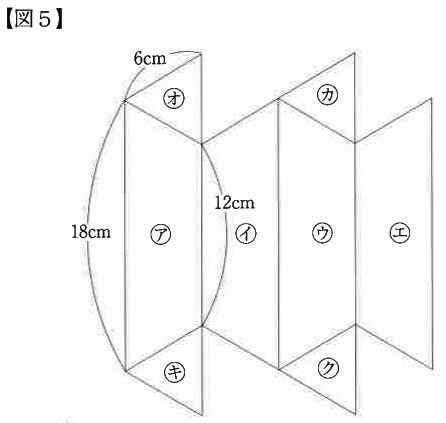
【図5】の展開図におい、(ア)~(エ)は合同な台形で、(オ)~(ク)は合同な正三角形です。この展開図を組み立てて立体を作ると、二種類の立体が作れます。そのうち、体積が大きい方の立体を立体C、体積が小さい方の立体を立体Dとします。2つの立体C、Dの体積の比(立体Cの体積):(立体Dの体積)を、最も簡単な整数の比で答えなさい。
@解説@
(1)

展開図で考えると三角錐のように思えるが…
もし三角錐だと頂点の切り落としのように断面が平面(斜線)になるはずなのに、
実際は凹んでいる!
等辺3cmの直角三角形の頂点3つが1点に交わるように凹ませるには、
斜線の平面からさらに織り込み、ふたたび同じ三角錐を内部につくる。
つまり、凹みの部分は合同な三角錐2つ分である。
6×6×6-3×3÷2×3÷3×2
=216-9=207cm3
(2)

組み立てるとアイスクリームみたいな形になる。
もう1種類の立体は、アイスの部分を(1)のように凹ませる。
この2つの立体の差を求める。

斜線の上と下の正四角錐は合同なので、上の正四角錐を出してから2倍する。
正三角形ABCの各辺を〇とする。
△CBEは等辺4cm、斜辺〇の直角二等辺三角形で、
これを1辺〇の正方形に4つあてはめると、対角線の長さは8cmとわかる。

斜辺〇、底辺4cm、90°より、★の直角二等辺三角形は合同→正四角錐の高さは4cm。
(底面の直角二等辺を立たせるイメージ)
体積の差は、8×8÷2×4÷3×2=256/3cm3
(3)

台形を凹ませると紙ぺらになりそうなので、凹れるポイントはサイドの正三角形。

体積ではなく体積比を求めるので、互いの上半分だけを考える。
辺の比は、12:18=2:3
断頭三角柱の考えを用いて、切断面が同じ正三角形だから3辺の高さの平均が体積比になる。
C:D=(2+3+3)/3:(3+2+2)/3
=8:7



コメント