問題PDF
(1)
1から6までの数字がそれぞれ書かれた、さいころAとさいころBがあります。さいころAの1つの面の上にシールをはり、シールに1から9のうちの1つの数字を選んでペンで書きます。このさいころとさいころBを同時に投げて出る数字の和をすべて調べてみると次のようになりました。
・最も大きい和は14
・最も小さい和は3
このとき、次の〔 〕にあてはまる数はいくつですか。
「Aの〔 あ 〕の面の上にシールをはり、シールに書いた数字は〔 い 〕」
(2)
1から6までの数字がそれぞれ書かれた、さいころCとさいころDがあります。それぞれのさいころの1つの面の上にシールをはり、シールに1から9のうちの1つの数字をそれぞれ選んでペンで書きます。これらのさいころを同時に投げて出る数字の和をすべて調べてみると次のようになりました。
・最も大きい和は16
・最も小さい和は3
・最も多く現れる和は9となる場合のみ
このとき次の〔 〕にあてはまる数はいくつですか。
ただし、〔 う 〕は〔 お 〕以下の数であるとします。
「Cの〔 う 〕の面の上にシールをはり、シールに書いた数字は〔 え 〕」
「Dの〔 お 〕の面の上にシールをはり、シールに書いた数字は〔 か 〕」
(3)
1から6までの数字がそれぞれ書かれた、さいころEとさいころFがあります。それぞれのさいころの1つの面の上にシールをはり、シールに1から9のうちの1つの数字をそれぞれ選んでペンで書きます。これらのさいころを同時に投げて出る数字の和をすべて調べてみると次のようになりました。
・最も大きい和は16
・最も小さい和は3
・最も多く現れる和は7と8となる場合のみ
このとき、次の〔 〕にあてはまる数はいくつですか。
ただし、〔 き 〕は〔 け 〕以下の数であるとします。
「Eの〔 き 〕の面の上にシールをはり、シールに書いた数字は〔 く 〕」
「Fの〔 け 〕の面の上にシールをはり、シールに書いた数字は〔 こ 〕」
@解説@
(1)
通常、2つのサイコロの和の最小値は1+1=2になるところ、
和の最小値が3ということは、Aの1の面が消されて何かに変わった。
和の最大値が14なので、14-6=8
Aの1を8に変えたことになる。
あ…1、い…8
(2)
和の最小値が3→どちらかの1にシール。
〔 う 〕は〔 お 〕以下なので、う=1
Cの1にシールを貼ったことになる。
3=1+2だから、Dの1は残す!
和の最大値は16→1~9の数字で和が16となる組み合わせは、
〔 え 〕+〔 か 〕=(7+9)(8+8)しかない。
つまり、シールに書かれる組み合わせは(7・9)か(8・8)のどちらか。
問題は、最も多く現れる和が9のみ。
→和が9となる組み合わせを最も多くする。
9=(1+8)(2+7)(3+6)(4+5)orこれらの逆。
7と8はシールを貼らないと作れない。
とりあえず、サイコロの3・4・5・6は残しておく。
→Dは2にシールを貼る。

◆(7・9)を貼る
C1→7、D2→9の場合、和が9となる場合が増えないので×。
C1→9、D2→7の場合、(2+7)が追加され、和が9は5通り。
しかし、頑張って調べてみると和が10も5通り!よって不適。
◆(8・8)を貼る
C1→8、D2→8。(8+1)が追加され、和が9は5通り。
和が8は4通り、和が10も4通り!
う…1、え…8、お…2、か…8
(3)
上2つの条件が同じなので、途中までは一緒。
和の最小が3で、〔 き 〕は〔 け 〕以下だから、〔 き 〕=1
Eの1にシールを貼り、Fの1は残す。
和の最大が16なので、貼る数字は(7・9)か(8・8)のどちらか。

ここからどうするか(;`ω´)
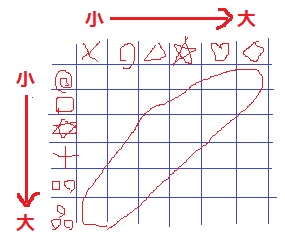
思うに、サイコロの和を表で示すと、斜めのラインに最も登場する和が現われる。
今、最も多く現われる和が7と8で、これらが同数となる。
7と8は連続する整数。
ということは、連番残しでは?
つまり、こちらの1番大きい数と向こうの1番小さい数を足す。
こちらの2番目に大きい数と向こうの2番目に小さい数を足す…
とやっていくと、同じ数がボコボコつくれるうえ、
7の和の組み合わせを1個ズラせば、8の和の組み合わせも作りやすいはず。

Eは1を消し、2~6が残る。
Fは1を残すことが決まっているので、反対側の6を消して1~5を残す。
この時点で、和が7は(2・5)(3・4)(4・3)(5・2)(6・1)の5通り。
和が8は(3・5)(4・4)(5・3)(6・2)の4通り。
Eの1を7、Fの6を9にすれば、和が8になる組み合わせに(1・7)が追加され、5通り。
ほかのパターンでは、和が8になる組み合わせが追加できない。
き…1、く…7、け…6、こ…9
*通常のサイコロを2つ振って、最も出やすい和は7。
これは6通りあるので、ここから条件に合う最多の組み合わせは5通りだと察する。



コメント