問題PDF
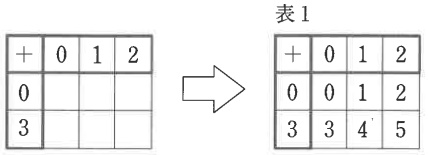
表の太枠部分(太い線で囲まれた部分)である上1行目と左1列目のマス目に0以上の整数を小さい順に書いた後、それ以外の細枠部分のマスそれぞれに対して、上1行目に書かれた数と横1列目に書かれた数の和を記入します。表1では上1行目に0、1、2、左1列目に0、3を書いて、和を記入して完成した表です。このとき、表1では、細枠部分に0から5までの数がすべてもれなく1度ずつ記入されています。
(1)
細枠部分に0から5までの数が1度ずつ現れるような表が、表1のほかにも考えられます。
その場合の上1行目3マスの数の配置を答えなさい。
(2)
表2のように上1行目の太枠部分4マス、左1列目の太枠部分2マスに数を書いた後に和を記入すると、細枠部分に0から7までの数が1度ずつ現れました。このような上1行目の数の配置を3通り答えなさい。
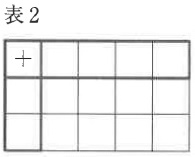
表3のように太枠部分が上1行目23マス、左1列目17マスの表があります。
(3)
和を記入すると、細枠部分に0から390までの数が重複することなく1つずつ現れるような太枠部分の数の配置は何通りありますか。
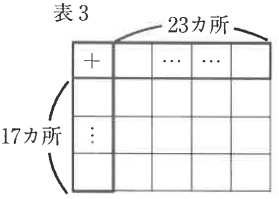
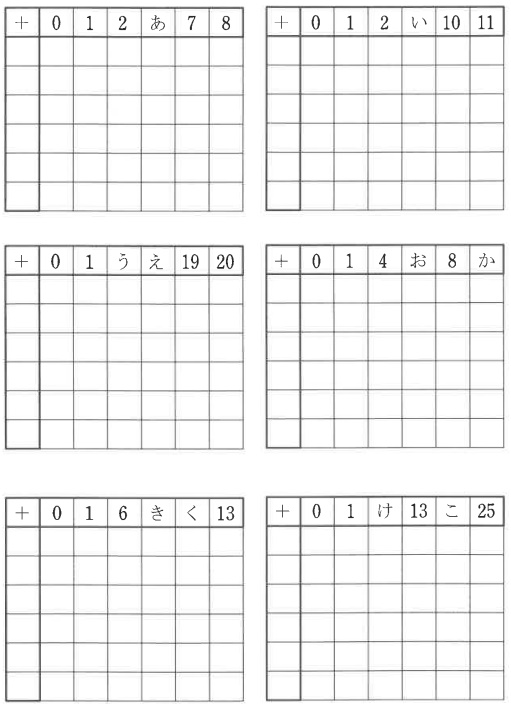
表4のように太枠部分が上1行目6マス、左1列目6マスの表で、和を記入すると、細枠部分に0から35までの数が1度ずつ現れるような配置を考えます。左1列目には1は含まれないこととすると、上1行目の太枠部分の数の配置は表5の例を含め全部で7通りあります。

(4)
空欄あ~こを埋めて上1行目の残りの6通りの配置をすべて答えなさい。
@解説@
(1)
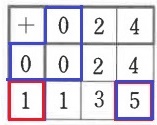
0を作るには0+0=0しかない。細枠の左上は0。
左1列目に1を入れてみる。重複を避けて2を作るには上1行目に2が入る。
細枠の右下は最大数5。残りを埋めていくと上1行目は(0、2、4)
(2)
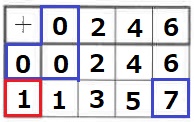
青枠は確定。赤枠を変えて埋めてみる。
赤枠=1として、重複を避けて2を作るには上1行目に2を入れる。
7の上は6。残りを埋めるとこのようになる。
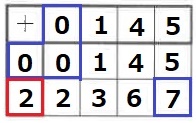
赤枠=2。1を作るのに上1行目に1…と順に埋めていく。
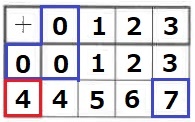
赤枠=3だと4が重複して6が作れない。
赤枠=4だと上図のようにうまくいく。
赤枠=5だと右下が8になってしまうので不適。
上1行目は(0、2、4、6)(0、1、4、5)(0、1、2、3)
(3)
難易度があがります。

今までの5つをボーと眺めてみると、上で作った固まりを加算して下の固まりができ、
下の固まりの最後の数字(最大数)が右上の最初の数字(最小数)につながるように見える…。
②、③の1行目は0、2、4…と数字が飛ぶ。
+1は数直線上で連続する整数。
1個ずつの固まりを上下で合わせると、(0、1)(2、3)(4、5)…と連なる。
①の1行目は(0、1、2)と連続する3つの整数。
+3で下の固まりは(3、4、5)
同様に、⑤も(0、1、2、3)で連続、これを+4すると下の固まり(4、5、6、7)
④は(0、1)(4、5)で連続性が分断される。
上(0、1)が+2されて下(2、3)。次は上(4、5)→下(6、7)と繋がる。
3行目以降の検証をしていないが…連続する固まりをつくるのがポイントだと思われる。

23は素数。2個ずつ…3個ずつ…の固まりはできない。
→固まりは1個ずつか23個ずつしかない。
答えは2通りとなる。

数字を埋めるとこのようになる。
(4)
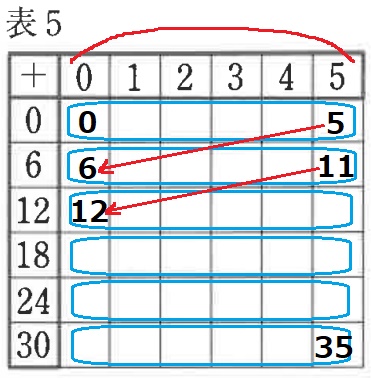
表5を確認しておくと、(0~5)の固まりが下へ降りていく。
固まりの最後5→次の固まりの最初6と連なる。
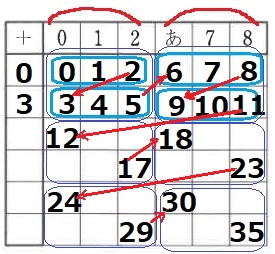
固まりは連続する整数である。
(0、1、2)で3個の固まり。同数の固まりで(あ、7、8)→あ=6
ある行までの小さな固まりを大きな固まりにくくる。
次の大きな固まりの最初が6→0~5の6個が大きな固まり。
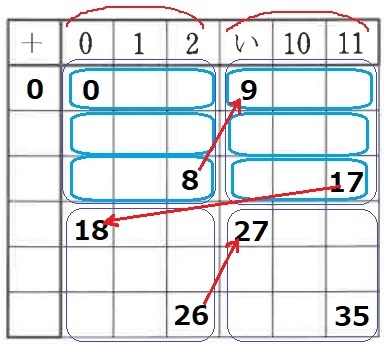
(0、1、2)(い、10、11)の3個ずつ→い=9
大きな固まりは0~8の9個。
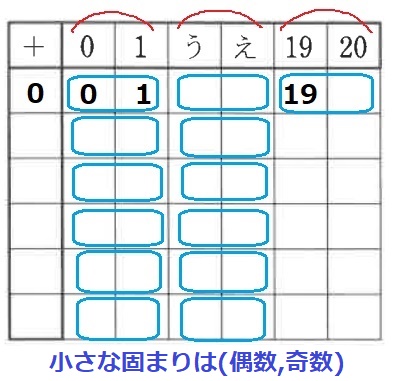
(0、1)(う、え)(19、20)と2個ずつの固まりにする。
大きな固まりをどのように区切っても小さな固まりは(0、1)のように
(偶数、奇数)の並びになる。19が固まりの左にあるので不適。
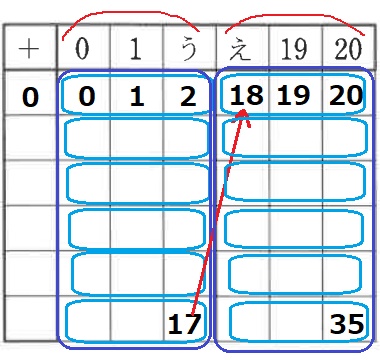
(0、1、う)(え、19、20)の固まり→う=2、え=18
大きい固まりは(0~17)の18個。
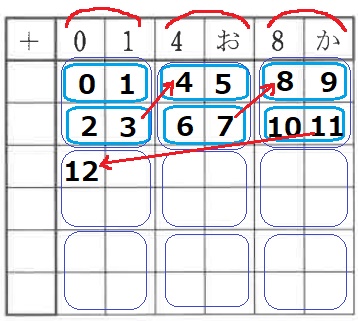
(0、1)(4、お)(8、か)→お=5、か=9
大きな固まりは4個ずつ。

仕組みさえわかればすぐ書けるが、試験時間内に読み解くのは厳しい。
き=7、く=12、け=12、こ=24
あ…6、い…9、う…2、え…18、お…5、か…9、き…7、く…12、け…12、こ…24



コメント