問題ＰＤＦ
（１）
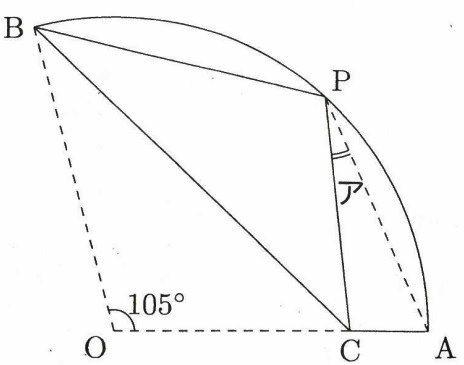
中心角が105°のおうぎ形の紙を、図のように折りました。
点Ｏが移った点をＰとすると、点Ｐはおうぎ形の周上にあります。
角アの大きさは何度ですか。
（２）
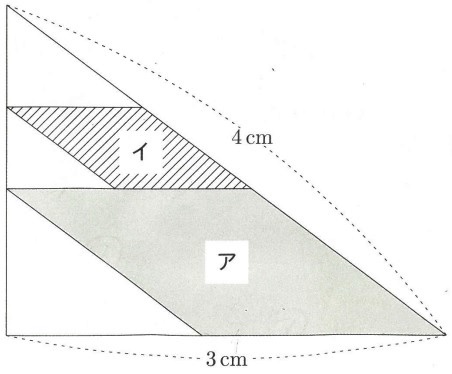
下の図のように、直角三角形にひし形アとひし形イがぴったりと入っています。
ひし形イの１辺の長さは何ｃｍですか。
（３）
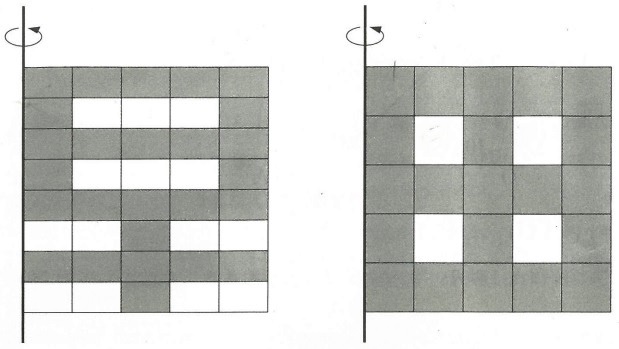
１辺が５ｃｍの正方形が２つあり、
たてとよこをそれぞれ等分割して「早」と「田」の字を書きました。
色の塗られた部分を図のように太線を軸にして１回転させた立体について、
「早」のつくる立体の体積は「田」のつくる立体の体積の何倍ですか。
＠解説＠
（１）
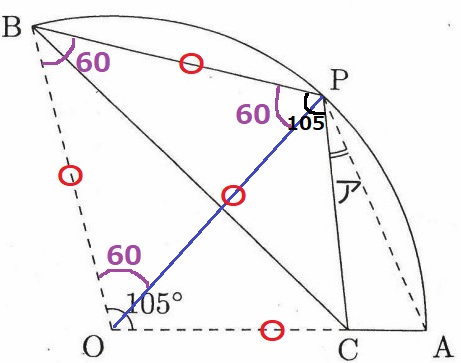
ＯＰに補助線。
半径より、ＯＢ＝ＯＰ＝ＯＡ
折り返しでＢＰも等しい。
△ＢＯＰは３辺が等しい正三角形。
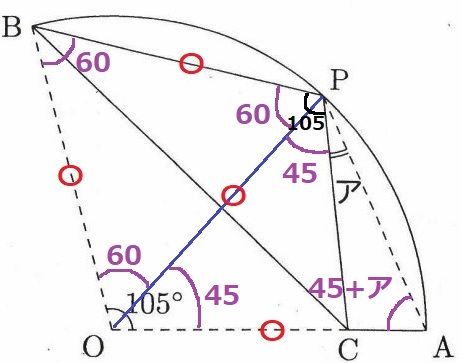
∠ＰＯＣ＝∠ＯＰＣ＝105－60＝45°
△ＯＡＰは二等辺三角形なので、
45＋（45＋ア）＋（45＋ア）＝180
２×ア＝45°
ア＝22.5°
（２）
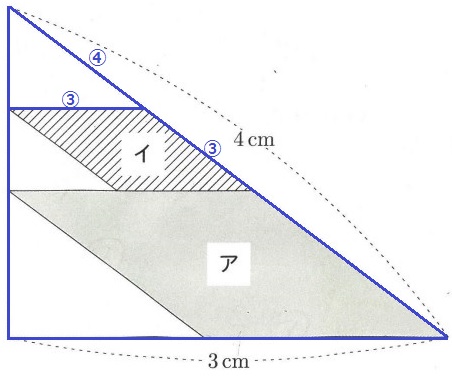
青腺の三角形は相似で、斜辺：底辺＝④：③
菱形イの１辺は③にあたり、これを斜辺側に移動させる。
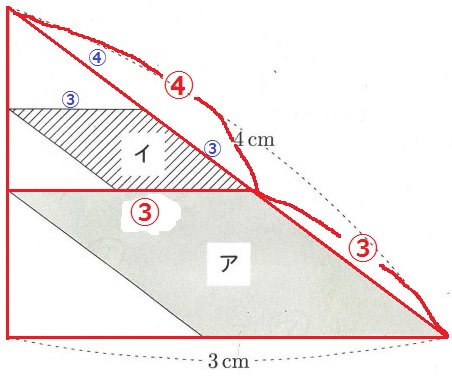
同様に、赤線の三角形も斜辺：底辺＝④：③
菱形アの１辺が③で、これを斜辺に移動させる。
菱形イの１辺③の長さは、４×④/⑦×③/⑦＝48/49ｃｍ
（３）
体積比でもいけますが、パップス・ギュルダンの定理を使います。
＠パップス・ギュルダンの定理＠
【回転体の体積＝断面積×重心の移動距離】
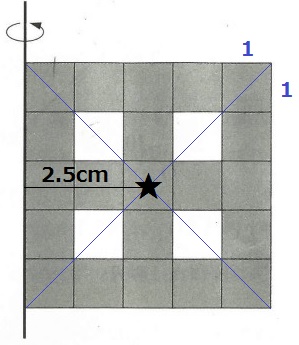
わかりやすい田から検討する。
断面積は、１×１×21＝21ｃｍ2
田は点対称図形だから重心は真ん中の★にあたる。軸から2.5ｃｍ離れている。
早の横は５等分だが、縦は８等分である点に注意！
断面積は、１×５/８×26＝130/８ｃｍ2
ブロックは縦にスライドすることができる。
なぜなら縦方向であればブロックの重心と軸との距離が変わらず、
そのブロックの回転体の体積も変わらないから。
上図のように早を縦にスライドして点対称に変形させると、
図形全体の重心と軸までの距離は田と同じ2.5ｃｍ。
軸との距離が変わらない＝重心の移動距離は変わらない。
ということは、回転体の体積比は断面積の比で決着する。
早：田＝130/８：21＝65：84
早の回転体の体積は田の回転体の65/84倍。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント