2021年度　豊島岡女子学園中学２回目過去問【算数】大問３解説

問題ＰＤＦ
（１）
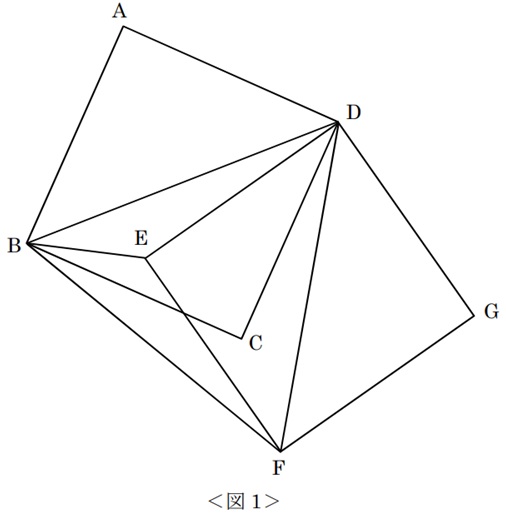
下の＜図１＞の正方形ＡＢＣＤと正方形ＤＥＦＧは合同です。
三角形ＢＤＦが正三角形となるとき、角ＥＢＣは何度ですか。

（２）
下の＜図２＞の正八角形ＡＢＣＤＥＦＧＨと正八角形ＨＩＪＫＬＭＮＯは合同です。
三角形ＤＨＬが正三角形となるとき、角ＪＤＥは何度ですか。

＠解説＠
（１）

正三角形と正方形が融合した図形なので、
どこかで２つの図形の情報を組み合わせられないかという発想に持っていく。

△ＢＤＥと△ＢＦＥに注目。
ＢＤ＝ＢＦ（正三角形の１辺）
ＥＤ＝ＥＦ（正方形の１辺）
ＢＥは共通辺。
３辺が等しいから、△ＢＤＥと△ＢＦＥは合同。

対応する角度は等しいので、∠ＤＢＥ＝∠ＦＢＥ＝60÷２＝30°
ＢＤは正方形の対角線。△ＢＣＤは直角二等辺三角形→∠ＤＢＣ＝45°
∠ＥＢＣ＝∠ＤＢＣ－∠ＤＢＥ＝45－30＝15°

（２）

（１）と同様に、正三角形と正八角形の情報を使う図形を考える。
ＪＨとＪＬに補助線をひき、先ほどと同じような形にする。
△ＤＨＪと△ＤＬＪにおいて、ＤＨ＝ＤＬ（正三角形の１辺）、ＤＪの共通辺。
ここで、△ＩＪＨと△ＫＪＬに注目する。
これらは正八角形の１辺を等辺、あいだの角を正八角形の内角とする二等辺三角形で合同。
ＪＨ＝ＪＬゆえ△ＤＨＪと△ＤＬＪは３辺が等しく、やはり合同。
対応する角から、∠ＨＤＪ＝60÷２＝30°
正八角形の４辺を延長すると、正八角形は正方形にスポっとおさまる。
四隅は直角二等辺三角形で、正八角形の内角は180－45＝135°
ＤＨに着目すると、ＤとＨは正八角形の中心をはさんで対極な位置関係にある。
対称性から、ＤＨは正八角形を合同に２等分する。
∠ＨＤＥ＝135÷２＝67.5°
∠ＪＤＥ＝∠ＨＤＥ－∠ＨＤＪ＝67.5－30＝37.5°

＠別解＠
なきいるかさんから、素晴らしい解法を頂きました。

正八角形のなかに四角形ＨＢＤＦと四角形ＨＪＬＮを結ぶと、
（１）と同じ構図が浮かび上がる！

∠ＪＤＦ＝15°は求めている。
∠ＦＤＥは二等辺三角形ＤＥＦの底角だから、
∠ＪＤＥ＝∠ＪＤＦ＋∠ＦＤＥ
＝15＋（180－135）÷２＝37.5°
*2018年の算数オリンピック決勝で似たような構図の問題が出題されたようです。
難関中（算数科）解説ページに戻る