問題ＰＤＦ
（１）
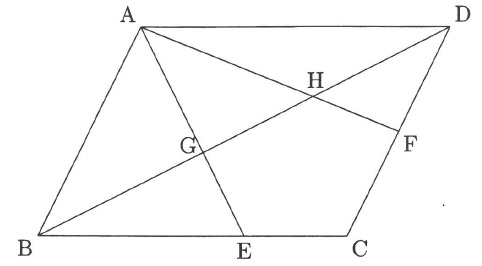
図の四角形ＡＢＣＤは、対角線ＢＤの長さが12ｃｍの平行四辺形で、
点Ｅは辺ＢＣを２：１に分ける点、点Ｆは辺ＣＤの真ん中の点です。
ＧＨの長さは何ｃｍですか。
（２）
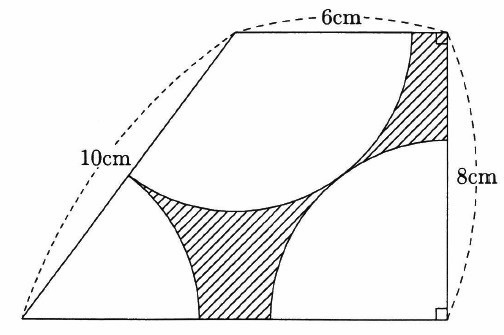
図の斜線部分は、台形から半径が同じおうぎ形３つを取り除いたものです。
斜線部分の面積は何ｃｍ2ですか。
（３）
図のように正三角形の紙を折りました。
紙が重なっている斜線部分の面積は何ｃｍ2ですか。
＠解説＠
難関中の世界ではわりとオーソドックスなので、
早稲田受験生は正解しておきたいところです。
（１）
ＡＦとＢＣの交点をＩとする。
ＡＥ：ＥＣ＝②：①、ＡＤ＝③
△ＡＧＤ∽△ＥＧＢ→辺の比は３：２
△ＡＨＤ∽△ＩＨＢ→辺の比は３：６＝１：２
辺ＢＤ上で連比して、ＢＧ：ＧＨ：ＨＤ＝６：４：５
１２×４/１５＝１６/５ｃｍ
（２）
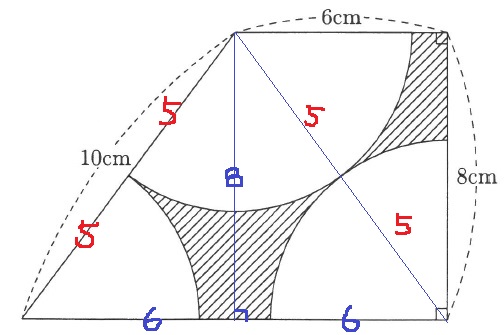
補助線をひくと、３：４：５の直角三角形があらわれる。
台形の下底は１２ｃｍとわかる。
半径は１０÷２＝５ｃｍ
扇形の中心角は左２つの和が180°（錯角で下ろすと一直線）なので、
３つの和は180＋90＝270°
（６＋１２）×８÷２－５×５×3.14×270/360
＝７２－58.875＝13.125ｃｍ2
（３）
角度を調べていく。
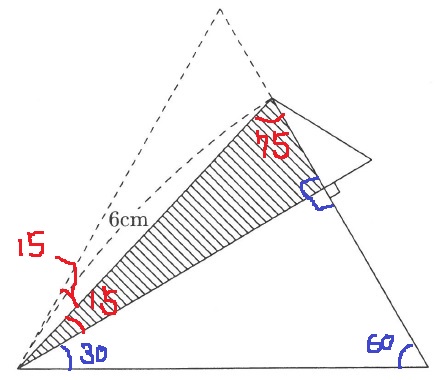
直角と６０°から左下が３０°。
折り返す角は、（６０－３０）÷２＝１５°
求積すべきは、斜辺が６ｃｍで15°－75°－90°の直角三角形。
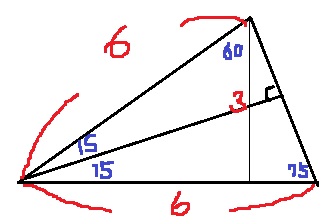
あとは中学受験でお馴染みのやり方。
合同図形をくっつけると、30°－75°－75°の二等辺になる。
補助線をひいて30°－60°－90°の直角三角形をつくり、高さは３ｃｍ。
６×３÷２÷２＝4.5ｃｍ2
難関中（算数科）解説ページに戻る
◆menu◆
公立高校入試…関東圏メイン。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント