問題ＰＤＦ
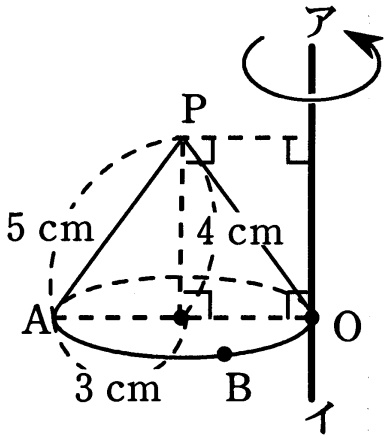
円すいと直線アイがあります。
円すいの体積は（底面積）×（高さ）÷３で求められます。
（１）
直線アイを軸として円すいを１回転させるとき、
円すいが通る部分の立体の体積と表面積を求めなさい。
（２）
円すいの側面（表面から底面を除いたもの）だけを考えます。
この側面を直線ＰＡとＰＯに沿って半分に切り分けたときの、点Ｂを含む方の曲面をＳとします。
直線アイを軸としてＳを180度だけ回転させるとき、Ｓが通る部分の立体の体積と表面積を求めなさい。
＠解説＠
（１）
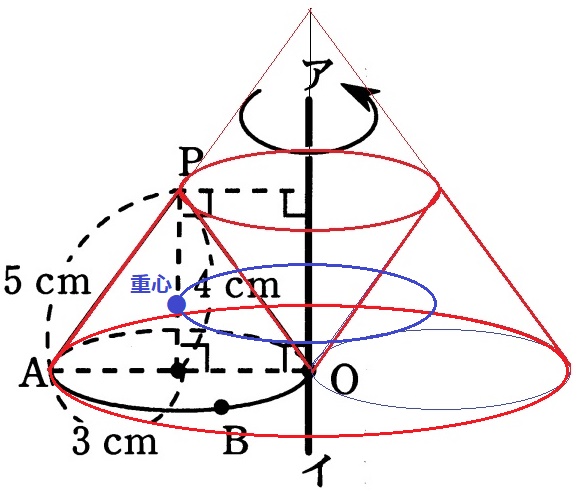
【パップス・ギュルダンの定理；回転体の体積＝断面積×重心の移動距離】
（＊くわしい原理は数Ⅲで習うようです）
断面積は△ＰＡＯの面積。その重心の移動距離は半径３ｃｍの円周。
６×４÷２×３×２×3.14＝72×3.14＝226.08ｃｍ3
延長して大きな円錐をつくる。
底面は半径６ｃｍの円。
小さい円錐と大きい円錐の相似比は５：10＝１：２
→真ん中の凹を上に持ち上げて凸にすると、大きな円錐の側面積に相当する。
【円錐の側面積＝半径×母線×3.14】
６×６×3.14＋６×10×3.14
＝96×3.14＝301.44ｃｍ2
体積…226.08ｃｍ3、表面積…301.44ｃｍ2
（２）
円錐の側面積の半分を180度回転する。
右図は上からみた様子で最初は空洞、最後は中身がある。
最後の中身を最初の空洞に突っ込むと、体積は（１）で求めた立体の半分になる。
226.08÷２＝113.04ｃｍ3
底面積は半径６ｃｍの半円。
中央部の凹の半周は先ほどのように持ち上げると、大きい円錐の側面積の半分に相当する。
ここまでは（１）で求めた立体の表面積の半分である。96×3.14÷２＝48×3.14
さらに、中に突っ込んだ小さい円錐の側面積が足される。３×５×3.14＝15×3.14
したがって、48×3.14＋15×3.14＝63×3.14＝197.82ｃｍ2
体積…113.04ｃｍ3、表面積…197.82ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント