問題ＰＤＦ
１円玉、５円玉、10円玉、50円玉、100円玉、500円玉の６種類のコインがそれぞれ３枚ずつあります。下の図のＡからＣの円の中にコインを１枚ずつ置いていきます。ただし、Ａの円に置くコインの金額は、ＢとＣの円に置くコインの金額の平均以下です。このとき、次の問いに答えなさい。
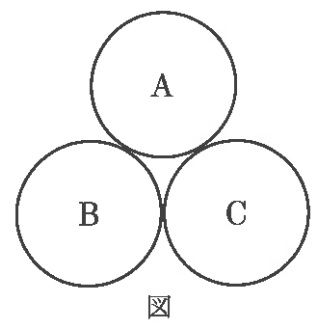
（１）
１円玉、５円玉、10円玉、50円玉の４種類のコインを１枚ずつ使えるとします。
その置き方は何通りありますか。
（２）
６種類のコインすべてを１枚ずつ使えるとします。
その置き方は何通りありますか。
（３）
６種類のコインすべてを３枚ずつ使えるとします。
その置き方は何通りありますか。
＠解説＠
（１）
条件は『Ａに置くコインは、ＢとＣのコインの金額の平均以下』
Ａのコインで場合分け使用しよう。
Ａ＝50円→最も高いので×
Ａ＝10円→（１、50）（５、50）＋これらの逆で４通り
Ａ＝５円→（１、10）（１、50）（10、50）＋逆で６通り
Ａ＝１円→（５、10）（５、50）（10、50）＋逆で６通り
計16通り
（２）
同様にＡで場合分け。
Ａ≦（Ｂ＋Ｃ）÷２
１・５・10・50・100・500の並びから、条件に適合するパターンを調べる。
Ａ＝500円→×
Ａ＝100円→500円は必ず使う。500円と残り４枚＋逆で８通り
Ａ＝50円
→500円と残り４枚＋逆で８通り
→500円を使わない。100円と残り３枚＋逆で６通り
計14通り
Ａ＝10円
→500円と残り４枚＋逆で８通り
→500円を使わずに、100円と残り３枚＋逆で６通り
→500円と100円を使わずに、50円と残り２枚＋逆で４通り
計18通り
Ａ＝５円
８＋６＋４＋２＝20通り
Ａ＝１円
８＋６＋４＋２＝20通り
計80通り
＠別解＠
【１・５・10・50・100・500】の並びで、Ａ＝１であれば、Ｂ・Ｃは何でもいい。
残りの５枚から２枚を選んで、Ｂ・Ｃに置く。
５×４＝20通り
Ａ＝５でも、ＢかＣに10円以上が必ず置かれるので条件成立。
５×４＝20通り
Ａ＝10円では、（Ｂ、Ｃ）＝（１、５）（５、１）がダメ。
20－２＝18通り
Ａ＝50円では、Ｂ・Ｃ双方に１・５・10円を置いてはダメ。
20－３×２＝14通り
Ａ＝100円では、Ｂ・Ｃ双方に１～50円がダメ。
20－４×３＝８通り
Ａ＝500円では、Ｂ・Ｃに何も置けない。
20＋20＋18＋14＋８＝80通り
（３）
前問で６種類のコインを１枚ずつ使った。
→Ａ・Ｂ・Ｃに置くコインはすべて異なる。
ということは、２枚だけ同種と３枚すべて同種の場合を足せばいい。
◆２枚同種
Ａ・Ｂが500円→Ｃには何も入らない→０通り
Ａ・Ｃが500円→同様に０通り
Ｂ・Ｃが500円→１～100円→５通り
計５通り
Ａ・Ｂが100円→Ｃは500円のみ→１通り
Ａ・Ｃが100円→１通り
Ｂ・Ｃが100円→Ａは500以外で４通り
計６通り
Ａ・Ｂが50円→Ｃは500円と100円→２通り
Ａ・Ｃが50円→２通り
Ｂ・Ｃが50円→Ａは１～10円→３通り
計７通り
Ａ・Ｂが10円→Ｃは50～500円→３通り
Ａ・Ｃが10円→３通り
Ｂ・Ｃが10円→Ａは１円か５円→２通り
計８通り
Ａ・Ｂが５円→Ｃは10～500円→４通り
Ｂ・Ｃが５円→４通り
Ａ・Ｃが５円→１円のみ→１通り
計９通り
Ａ・Ｂが１円→Ｃは５～500円→５通り
Ｂ・Ｃが１円→５通り
Ａ・Ｃが１円→なし
計10通り
５＋６＋７＋８＋９＋10＝45通り
◆３種同種
１～500それぞれで６通り
よって、80＋45＋６＝131通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント