2018年度　豊島岡女子学園中学過去問【算数】大問６解説

問題ＰＤＦ
１辺の長さが５ｃｍの立方体ＡＢＣＤ－ＥＦＧＨがあります。
また、辺ＣＧ上に点Ｐがあり、ＰＧの長さは１ｃｍです。
このとき、次の各問いに答えなさい。

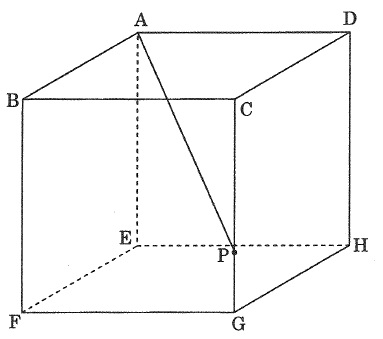
（１）
辺ＢＦ上に点Ｑがあり、ＢＱの長さが１ｃｍです。
また、ＤＨ上に点Ｒがあり、２つのＡＰ、ＱＲは交わっています。
このとき、ＨＲの長さは何ｃｍですか。

（２）
辺ＢＦ、ＤＨ上に動く点Ｓ、Ｔがあり、２つの直線ＡＰ、ＳＴは交わっています。
その点をＵとするとき、四角すいＵ－ＥＦＧＨの体積は何ｃｍ³ですか。

（３）
辺ＣＤ上に点Ｖがあり、ＤＶの長さが１ｃｍです。
また、辺ＥＦ上に点Ｗがあり、２つの直線ＡＰ、ＶＷは交わっています。
その点をＸとするとき、四角すいＸ－ＥＦＧＨの体積は何ｃｍ³ですか。

＠解説＠
面白い設問だが･･･難しい(´ﾟдﾟ｀)
（１）

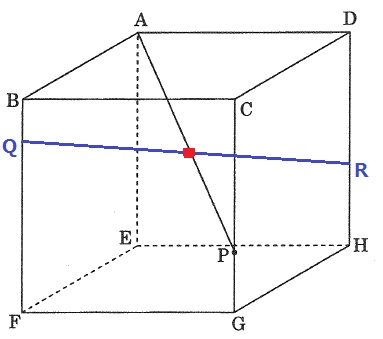
ＱＲが●で交わるときのＨＲを求めたい。
なんとなく●は中点で交わっていそう…。

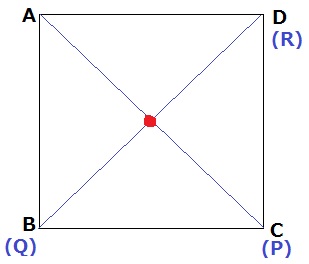
上からみると、●は正方形の対角線の交点にある。
上から見る平面図では高さを無視し、ＡＰとＱＲの長さは異なるが、
ＡＰとＱＲが正方形の真ん中で交わるということは、●はＡＰ、ＱＲの中点にある。

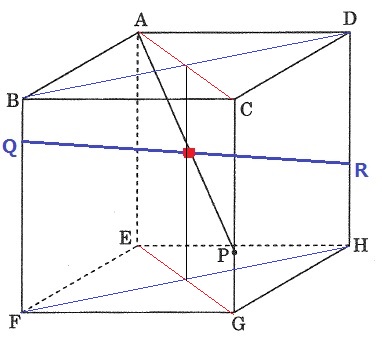
立体でみると面ＡＥＧＣ上にＡＰ、面ＢＦＨＤ上にＱＲがあり、
ＡＰとＱＲの交点●は面ＡＥＧＣと面ＢＦＨＤの交線上にある→正方形の真ん中

面ＡＥＧＣではＡ→Ｐで４ｃｍ下がるので、Ａ→●まで２ｃｍ下がる。
●の高さは３ｃｍ。
面ＢＦＨＤ上の●も高さが３ｃｍ。
Ｑ→●で１ｃｍ下がるので、●→Ｒも１ｃｍ下がる。

（２）
ＳはＢＦ上を、ＴはＤＨ上を動くという…。
四角錘Ｕ－ＥＦＧＨの体積を求めるためには、Ｕから垂線を下ろしたときの高さが知りたい。
ということは、ＳとＴが動いてもＵの位置は変化しないのでは？と推測する。

立方体において、辺ＢＦと辺ＤＨは対辺である。
（１）のように、上からみた平面図ではＡＰとＳＴは正方形の対角線であり、
各々中点で交わるはず。

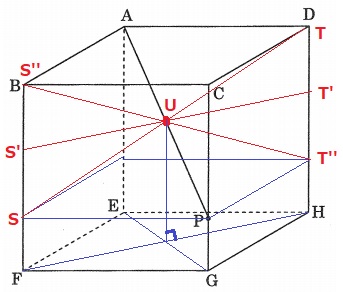
上の図で、Ｓより下だと、ＳＴの中点がＵより下にくるのでＡＰと交わらない。
Ｔ”より下だと、Ｓ”Ｔ’’の中点がＵより下にくるのでＡＰと交わらない。
ＳとＴは高さ１ｃｍ以上にあり、互いが反対側にあればＳＴはＡＰと中点Ｕで交わる。

結局、Ｕは（１）の●と同じ位置にある。
→四角錘の高さは３ｃｍ。
よって、四角錘Ｕ－ＥＦＧＨの体積は、５×５×３÷３＝25ｃｍ³

（３）
難問です。

今までは上からみたときに２直線が正方形の対角線となり、
各々の中点で交わってくれたが、本問のＶはＤから１ｃｍズレている！
ＸはＵのようにＡＰの中点ではない。
……かなり悩みました(;´～｀)

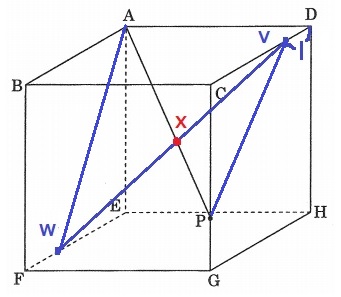
ＡＷとＶＰをひいてみる。
なんか、△ＡＸＷと△ＶＸＰが相似っぽく見える。。。

（１）では、上からみるとＡＰとＱＲの交点が中点にあり、
上からみて１：１で、横からみても１：１だった。
ということは、立方体の内部にある直線を上から見たときの長さの比は、
横から見たときの長さの比と同じになるのでは？

左の図は、ＡＰとＶＷの位置関係を立方体の上面に写し取ったもの。
Ｗ→Ｗ’、Ｘ→Ｘ’、Ｐ→Ｃに移動。
真上から下へ視線を下ろしているので、Ｗ’とＷ、Ｘ’とＸはかぶっており、
Ｗ’ＷとＸ’Ｘは底面に対して垂直で、互いに平行。
△Ｗ’ＷＶ∽△Ｘ’ＸＶから、Ｗ’Ｘ’：Ｘ’Ｖ＝ＷＸ：ＸＶ
△ＡＸ’Ｘ∽△ＡＣＰから、ＡＸ’：Ｘ’Ｃ＝ＡＸ：ＸＰ

右の図は、ＡＰとＶＷの位置関係を立方体の正面に写し取ったもの。
Ａ→Ｂ、Ｗ→Ｆ、Ｘ→Ｘ’’、Ｖ→Ｃに移動。
ＷＦとＸＸ’’は正面から見たときに線分として目に見えず、奥行きとしてＡＢやＶＣと平行である。
ＷＦ//ＸＸ’’//ＶＣから平行線と線分の比で、ＦＸ”：Ｘ’’Ｃ＝ＷＸ：ＸＶ
△ＡＰＢ∽△ＸＰＸ’’から、ＢＸ’’：Ｘ’’Ｐ＝ＡＸ：ＸＰ
このように、空間に浮かぶ２直線ＡＰとＶＷの位置関係は、２つの平面に写しとることができる。

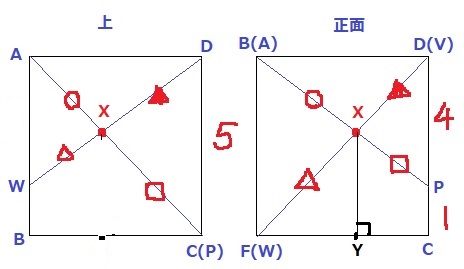
求めたい四角錘の高さがわかるのは、正面から見た図。
Ｘから垂線をおろし、交点をＹとする。
ＸＹが四角錘Ｘ－ＥＦＧＨの高さにあたる。
△ＢＸＦ∽△ＰＸＤより、ＦＸ：ＸＤ＝ＢＦ：ＰＤ＝５：４
△ＸＹＦ∽△ＤＣＦより、ＸＹ＝５×５/９＝25/９ｃｍ

したがって、四角錘Ｘ－ＥＦＧＨの体積は、
５×５×25/９÷３＝625/27ｃｍ³
*実際の入試では細かい説明を抜きにして、
前問の結果から上からや正面からの図に置き換えて相似を使ってもよいのでは？
と想像し、とりあえず計算して解答用紙に書いてみる…でよいと思う。
難関中（算数科）解説ページに戻る